
题目列表(包括答案和解析)
若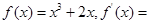 _________________;
_________________;
若 ;
;
求:(1)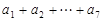 ;
;
(2)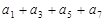 ;
;
(3)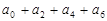 ;
;
若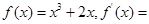 _________________;
_________________;
 _________________;
_________________;若![]() ;
;
![]() .
.
一、选择题(每小题5 分,共40 分)
DACDA DBA
二、填空题(每小题5 分,共35分)
9. 10.400 11.180 12.②④
10.400 11.180 12.②④
13. 14.(i)
14.(i) (3分) (ii)
(3分) (ii) (2分)
(2分)
15.(i) (3分); (ii)
(3分); (ii) (2分)
(2分)
16.(1)

当
 ……………………4分
……………………4分
(2)令 ………………6分
………………6分
解得:
所以, 的单调递增区间是
的单调递增区间是 …………8分
…………8分
(3)由 ,……………………10分
,……………………10分
所以,
解得:
所以, 的取值集合
的取值集合 ……12分
……12分
17.解:(1)坐A 班车的三人中恰有2 人正点到达的概率为
P3(2)=
C 0.72×0.31 =
0.441 ……………………(6
分)
0.72×0.31 =
0.441 ……………………(6
分)
(2)记“A 班车正点到达”为事件M,“B 班车正点到达冶为事件N
则两人中至少有一人正点到达的概率为
P
= P(M?N)+
P(M? )+ P(
)+ P( ?N)
?N)
= 0.7 ×0.75 + 0.7 ×0.25 + 0.3 ×0.75 = 0.525 + 0.175 + 0.225 = 0.925 (12 分)
18.解:由已知得
所以数列{ }是以1为首项,公差为1的等差数列;(2分)
}是以1为首项,公差为1的等差数列;(2分)
即 =1+
=1+ …………………………4分
…………………………4分
(2)由(1)知 ……………………6分
……………………6分


 …………………………8分
…………………………8分

 ……………………10分
……………………10分
所以: …………………………12分
…………………………12分
19.解:M、N、Q、B的位置如右图示。(正确标出给1分)
(1)∵ND//MB且ND=MB
∴四边形NDBM为平行四边形
∴MN//DB………………3分
∴BD 平面PBD,MN
平面PBD,MN
∴MN//平面PBD……………………4分
(2)∵QC⊥平面ABCD,BD 平面ABCD,
平面ABCD,
∴BD⊥QC……………………5分
又∵BD⊥AC,
∴BD⊥平面AQC…………………………6分
∵AQ 面AQC
面AQC
∴AQ⊥BD,同理可得AQ⊥PB,
∵BD PD=B
PD=B
∴AQ⊥面PDB……………………………8分
|