
题目列表(包括答案和解析)
命题“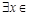 R,
R,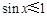 ”的否定是 .
”的否定是 .
 R,
R, ”的否定是 .
”的否定是 .命题“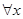 ∈R,
∈R,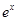 -x+1≥0”的否定是( )
-x+1≥0”的否定是( )
A.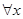 ∈R,lnx+x+1<0 ∈R,lnx+x+1<0 | B. ∈R, ∈R,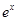 -x+1<0 -x+1<0 |
C.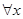 ∈R, ∈R,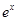 -x+1>0 -x+1>0 | D. ∈R, ∈R,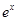 -x+1≥0 -x+1≥0 |
 ”的否定是 .
”的否定是 . ”的否定是 .
”的否定是 .
必做题部分
一、填空题:本大题共14小题,每小题5分,共70分.
【填空题答案】
1. R,
R, ;
2.3;
3.1;
4.5;
5.
;
2.3;
3.1;
4.5;
5. ;
;
6.2;
7.y=2x+3; 8.1.5; 9. ;
10.
;
10. ;
;
11.充要;
12.-1; 13. ; 14.2.
; 14.2.
二、解答题:本大题共6小题,共90分. 解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
△ABC的外接圆半径为1,角A,B,C的对边分别为a,b,c.向量m = ,
,
n= 满足m//n.
满足m//n.
(1)求 的取值范围;
的取值范围;
(2)若实数x满足abx=a+b,试确定x的取值范围.
【解】(1)因为m//n, 所以 ,
, ………………………2分
………………………2分
因为三角形ABC的外接圆半径为1, 由正弦定理,得 .
.
于是 .
.
因为 . 故三角形ABC为直角三角形. ………………………5分
. 故三角形ABC为直角三角形. ………………………5分
 , 因为
, 因为 ,
,
所以 , 故
, 故 . ………………………7分
. ………………………7分
(2) .
………………………9分
.
………………………9分
设 ,则
,则 ,
…………………… 11分
,
…………………… 11分
 ,因为
,因为 <0,故
<0,故 在(1,
在(1, ]上单调递减函数.
]上单调递减函数.
所以
 .所以实数x的取值范围是
.所以实数x的取值范围是 .
…………………… 14分
.
…………………… 14分
16.(本小题满分14分)
 在四棱锥P-ABCD中,四边形ABCD是梯形,AD∥BC,∠ABC=90°,平面PAB⊥平面ABCD,
在四棱锥P-ABCD中,四边形ABCD是梯形,AD∥BC,∠ABC=90°,平面PAB⊥平面ABCD,
平面PAD⊥平面ABCD.
(1)求证:PA⊥平面ABCD;
(2)若平面PAB 平面PCD
平面PCD ,问:直线l能否与平面ABCD平行?
,问:直线l能否与平面ABCD平行?
请说明理由.
(1)【证明】因为∠ABC=90°,AD∥BC,所以AD⊥AB.
而平面PAB⊥平面ABCD,且平面PAB 平面ABCD=AB,
平面ABCD=AB,
所以AD⊥平面PAB, 所以AD⊥PA. ………………3分
同理可得AB⊥PA. ………………5分
由于AB、AD 平面ABCD,且AB
平面ABCD,且AB AD=C,
AD=C,
所以PA⊥平面ABCD. ………………………7分
(2)【解】(方法一)不平行. ………………………9分
证明:假定直线l∥平面ABCD,
由于l 平面PCD,且平面PCD
平面PCD,且平面PCD 平面ABCD=CD, 所以
平面ABCD=CD, 所以 ∥CD. ……………………
11分
∥CD. ……………………
11分
同理可得l∥AB, 所以AB∥CD. …………………… 13分
这与AB和CD是直角梯形ABCD的两腰相矛盾,
故假设错误,所以直线l与平面ABCD不平行. …………………… 14分
(方法二)因为梯形ABCD中AD∥BC,
所以直线AB与直线CD相交,设AB CD=T.
…………………… 11分
CD=T.
…………………… 11分
由T CD,CD
CD,CD 平面PCD得T
平面PCD得T 平面PCD.
平面PCD.
同理T 平面PAB.
…………………… 13分
平面PAB.
…………………… 13分
即T为平面PCD与平面PAB的公共点,于是PT为平面PCD与平面PAB的交线.
所以直线 与平面ABCD不平行.
…………………… 14分
与平面ABCD不平行.
…………………… 14分
17.(本小题满分15分)
设a为实数,已知函数 .
.
(1)当a=1时,求函数 的极值.
的极值.
(2)若方程 =0有三个不等实数根,求a的取值范围.
=0有三个不等实数根,求a的取值范围.
【解】(1)依题有 ,
,
故 .
………………………2分
.
………………………2分
由
x

0

2


+
0
-
0
+

ㄊ
极大值
ㄋ
极小值
ㄊ
………………………5分
得 在
在 时取得极大值
时取得极大值 ,
, 在
在 时取得极小值
时取得极小值 . …………7分
. …………7分
(2) 因为 ,
………………………9分
,
………………………9分
所以方程 的两根为a-1和a+1,
的两根为a-1和a+1,
显然,函数 在x= a-1取得极大值,在x=a+1是取得极小值. …………………… 11分
在x= a-1取得极大值,在x=a+1是取得极小值. …………………… 11分
因为方程 =0有三个不等实根,
=0有三个不等实根,
所以 即
即 解得
解得 且
且 .
.
故a的取值范围是 .
…………………… 15分
.
…………………… 15分
18.(本小题满分15分)
如图,椭圆 (a>b>0)的左、右焦点分别为F1、F2,M、N是椭圆右准线上的两个动点,
(a>b>0)的左、右焦点分别为F1、F2,M、N是椭圆右准线上的两个动点,
 且
且 .
.
(1)设C是以MN为直径的圆,试判断原点O与圆C的位置关系;
(2)设椭圆的离心率为 ,MN的最小值为
,MN的最小值为 ,求椭圆方程.
,求椭圆方程.
【解】(1)设椭圆 的焦距为
的焦距为
则其右准线方程为x= ,且F1(-c, 0), F2(c,
0). ……………2分
,且F1(-c, 0), F2(c,
0). ……………2分
设M ,
,
则 =
=
 .
………………………4分
.
………………………4分
因为 ,所以
,所以 ,即
,即 .
.
于是 ,故∠MON为锐角.
,故∠MON为锐角.
所以原点O在圆C外. ………………………7分
(2)因为椭圆的离心率为 ,所以a=
,所以a=
于是M  ,且
,且 ………………………9分
………………………9分
MN2=(y1-y2)2=y12+y22-2y1y2 . …………………… 12分
. …………………… 12分
当且仅当 y1=-y2= 或y2=-y1=
或y2=-y1= 时取“=”号, ……………………
13分
时取“=”号, ……………………
13分
所以(MN)min=
故所求的椭圆方程是 .
…………………… 15分
.
…………………… 15分
19.(本小题满分16分)
下述数阵称为“森德拉姆筛”,记为S.其特点是每行每列都是等差数列,第i行第j列的数记为
Aij.
1 4 7 10 13 …
4 8 12 16 20 …
7 12 17 22 27 …
10 16 22 28 34 …
13 20 27 34 41 …
… … … …
(1)证明:存在常数 ,对任意正整数i、j,
,对任意正整数i、j, 总是合数;
总是合数;
(2)设 S中主对角线上的数1,8,17,28,41,…组成数列 . 试证不存在正整数k和m
. 试证不存在正整数k和m
 ,使得
,使得 成等比数列;
成等比数列;
(3)对于(2)中的数列 ,是否存在正整数p和r
,是否存在正整数p和r  ,使得
,使得 成等差
成等差
数列.若存在,写出 的一组解(不必写出推理过程);若不存在,请说明理由.
的一组解(不必写出推理过程);若不存在,请说明理由.
(1)【证明】因为第一行数组成的数列{A1j}(j=1,2,…)是以1为首项,公差为3的等差数列,
所以A1 j=1+(j-1)×3=3 j-2,
第二行数组成的数列{A2j}(j=1,2,…)是以4为首项,公差为4的等差数列,
所以A2 j=4+(j-1)×4=4 j. ………………………2分
所以A2 j-A1 j=4 j-(3 j-2)=j+2,
所以第j列数组成的数列{ Aij}(i=1,2,…)是以3 j-2为首项,公差为 j+2的等差数列,
所以Aij=3 j-2+(i-1) ×(j+2) =ij+2i+2j-4
=(i+3) (j+2) 8. ……………5分
故Aij+8=(i+3) (j+2)是合数.
所以当 =8时,对任意正整数i、j,
=8时,对任意正整数i、j, 总是合数
………………………6分
总是合数
………………………6分
(2)【证明】(反证法)假设存在k、m, ,使得
,使得 成等比数列,
成等比数列,
即 ………………………7分
………………………7分
∵bn=Ann =(n+2)2-4
∴
得 ,
,
即 ,
………………………10分
,
………………………10分
又∵ ,且k、m∈N,∴k≥2、m≥3,
,且k、m∈N,∴k≥2、m≥3,
∴ ,这与
,这与 ∈Z矛盾,所以不存在正整数k和m
∈Z矛盾,所以不存在正整数k和m ,使得
,使得 成等比数列.……………………12分
成等比数列.……………………12分
(3)【解】假设存在满足条件的 ,那么
,那么
即 .
…………………… 14分
.
…………………… 14分
不妨令 得
得
所以存在 使得
使得 成等差数列.
…………………… 16分
成等差数列.
…………………… 16分
(注:第(3)问中数组 不唯一,例如
不唯一,例如 也可以)
也可以)
20.(本小题满分16分)
如果对任意一个三角形,只要它的三边长a,b,c都在函数f(x)的定义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“保三角形函数”.
(1)判断下列函数是不是“保三角形函数”,并证明你的结论:
① f(x)= ; ② g(x)=sinx (x∈(0,π)).
(2)若函数h(x)=lnx (x∈[M,+∞))是保三角形函数,求M的最小值.
(1)【答】f(x)= 是保三角形函数,g(x)=sinx (x∈(0,π))不是保三角形函数.
【证明】① f(x)= 是保三角形函数.
对任意一个三角形的三边长a,b,c,则a+b>c,b+c>a,c+a>b,
f(a)= ,f(b)= ,f(c)= .
因为(+)2=a+2+b>c+2>()2,所以+>.
同理可以证明:+>,+>.
所以f(a)、f(b)、f(c)也是某个三角形的三边长,故 f(x)= 是保三角形函数. ………………4分
②g(x)=sinx (x∈(0,π))不是保三角形函数. 取 ,显然这三个数能作为一个
,显然这三个数能作为一个
三角形的三条边的长. 而sin =1,sin
=1,sin =,不能作为一个三角形的三边长.
=,不能作为一个三角形的三边长.
所以g(x)=sinx (x∈(0,π))不是保三角形函数. ………………………8分
(2)【解】M的最小值为2. …………………… 10分
(i)首先证明当M≥2时,函数h(x)=lnx (x∈[M,+∞))是保三角形函数.
对任意一个三角形三边长a,b,c∈[M,+∞),且a+b>c,b+c>a,c+a>b,
则h(a)=lna,h(b)=lnb,h(c)=lnc.
因为a≥2,b≥2,a+b>c,所以(a-1)(b-1)≥1,所以ab≥a+b>c,所以lnab>lnc,
即lna+lnb>lnc.
同理可证明lnb+lnc>lna,lnc+lna>lnb.
所以lna,lnb,lnc是一个三角形的三边长.
故函数h(x)=lnx (x∈[M,+∞),M≥2),是保三角形函数. …………………… 13分
(ii)其次证明当0<M<2时,h(x)=lnx (x∈[M,+∞))不是保三角形函数.
当0<M<2时,取三个数M,M,M2∈[M,+∞),
因为0<M<2,所以M+M=2M>M2,所以M,M,M2是某个三角形的三条边长,
而lnM+lnM=2lnM=lnM2,所以lnM,lnM,lnM2不能为某个三角形的三边长,
所以h(x)=lnx 不是保三角形函数.
所以,当M<2时,h(x)=lnx (x∈[M,+∞))不是保三角形函数.
综上所述:M的最小值为2. …………………… 16分
附加题部分
21. (选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
E.
 选修4-1:几何证明选讲
选修4-1:几何证明选讲
如图,PA切⊙O于点 ,D为
,D为 的中点,过点D引
的中点,过点D引
割线交⊙O于 、
、 两点.求证:
两点.求证:  .
.
【证明】因为 与圆相切于
与圆相切于 ,
,
所以 , ………………………2分
, ………………………2分
因为D为PA中点,所以DP=DA,
所以DP2=DB?DC,即 . ………………………5分
. ………………………5分
因为 ,
所以
,
所以 ∽
∽ ,
………………………8分
,
………………………8分
所以 . ……………………
10分
. ……………………
10分
F. 选修4-2:矩阵与变换
已知在一个二阶矩阵M的变换作用下, 点 变成了点
变成了点 ,点
,点 变成了点
变成了点
 ,求矩阵M.
,求矩阵M.
【解】设 ,
………………………2分
,
………………………2分
则由 ,
, ,
………………………5分
,
………………………5分
得 ………………………8分
………………………8分
所以 因此
因此 .
…………………… 10分
.
…………………… 10分
G. 选修4-4:坐标系与参数方程
在极坐标系中,已知圆C的圆心坐标为C (2, ),半径R=
),半径R= ,求圆C的极坐标方程.
,求圆C的极坐标方程.
解法一:设P(ρ,θ)是圆上的任意一点,则PC=
R= . ……………………4分
. ……………………4分
由余弦定理,得ρ2+22-2×2×ρcos(θ- )=5.
……………………8分
)=5.
……………………8分
化简,得ρ2-4ρcos(θ- )+1=0,此即为所求的圆C的方程. ……………………10分
)+1=0,此即为所求的圆C的方程. ……………………10分
解法二:将圆心C (2, )化成直角坐标为(1,
)化成直角坐标为(1, ),半径R=
),半径R= ,
……………………2分
,
……………………2分
故圆C的方程为(x-1)2+(y- )2=5.
……………………4分
)2=5.
……………………4分
再将C化成极坐标方程,得(ρcosθ-1)2+(ρcosθ- )2=5. ……………………6分
)2=5. ……………………6分
化简,得ρ2-4ρcos(θ- )+1=0 ,此即为所求的圆C的方程. ……………………10分
)+1=0 ,此即为所求的圆C的方程. ……………………10分
H. 选修4-5:不等式选讲
已知 ,求证:
,求证: .
.
【证明】因为 ………………………3分
………………………3分
 ………………………7分
………………………7分
所以 .
.
故 .
…………………… 10分
.
…………………… 10分
22. 必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
投掷A,B,C三个纪念币,正面向上的概率如下表所示 .
.
纪念币
A
B
C
概 率

a
a
将这三个纪念币同时投掷一次, 设 表示出现正面向上的个数.
表示出现正面向上的个数.
(1)求 的分布列及数学期望;
的分布列及数学期望;
(2)在概率 (i=0,1,2,3)中, 若
(i=0,1,2,3)中, 若 的值最大, 求a的取值范围.
的值最大, 求a的取值范围.
【解】(1) 是
是 个正面向上,
个正面向上, 个背面向上的概率.其中
个背面向上的概率.其中 的可能取值为0,1,2,3.
的可能取值为0,1,2,3.
 ,
,
 ,
,
 ,
,
 .
………………………4分
.
………………………4分
所以 的分布列为
的分布列为










 的数学期望为
的数学期望为
 .
………………………5分
.
………………………5分
(2)  ,
,
 ,
,
 .
.
由 和
和 ,得
,得 ,即a的取值范围是
,即a的取值范围是 . …………………… 10分
. …………………… 10分
23.必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
已知 .用数学归纳法证明:
.用数学归纳法证明: .
.
【证明】(1)当n=2时,左边-右边= ,不等式成立.
,不等式成立.
………………………2分
(2)假设当n=k( )时,不等式成立,即
)时,不等式成立,即
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com