某射击比赛规则是:开始时在距离目标100米处射击.如果命中记3分.同时停止射击,若第一次射击未命中目标.则可以进行第二次射击.但目标已在150米远处.这是命中记2分.同时停止射击,若第二次射击仍未命中——青夏教育精英家教网—

某射击比赛规则是:开始时在距离目标100米处射击.如果命中记3分.同时停止射击,若第一次射击未命中目标.则可以进行第二次射击.但目标已在150米远处.这是命中记2分.同时停止射击,若第二次射击仍未命中目标.还可以进行第三次射击.此时目标已在200米远处.这时命中记1分.同时停止射击,若三次射击都未命中目标.则记0分.已知甲射手在100米处击中目标的概率是.他命中目标的概率与距离的平方成反比.且各次射击是相互独立的.(1) 求射手甲分别在150米和200米处命中目标的概率, 【查看更多】

题目列表(包括答案和解析)

某射击比赛规则如下，开始时在距目标100米处射击，如果命中记3分，且停止射击；若第一次射击未命中，可以进行第二次射击，但目标已在150米处，这时命中记2分，且停止射击；若第二次仍未命中还可以进行第三次射击，但此时目标已在200米处，若第三次命中则记1分，并停止射击；若三次都未命中，则记0分，已知某射手在100米处击中目标的概率为，他的命中率与目标距离的平方成反比，且各次射击都是相互独立的

（1）求这名射手在射击比赛中命中目标的概率；

（2）若这名射手在射击比赛中得分记为，求的分布列与数学期望．

查看答案和解析>>

.（满分12分）某射击比赛，开始时在距目标100米处射击，如果命中记3分，且停止射击；若第一次射击未命中，可以进行第二次射击，但目标已在150米处，这时命中记2分，且停止射击；若第二次仍未命中还可以进行第三次射击，但此时目标已在200米处，若第三次命中则记1分，并停止射击；若三次都未命中，则记0分。已知射手在100米处击中目标的概率为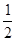，他的命中率与目标距离的平方成反比，且各次射击都是独立的。

（1）求这名射手在射击比赛中命中目标的概率；

（2）求这名射手在比赛中得分的数学期望。

查看答案和解析>>

某种项目的射击比赛，开始时在距目标100米处射击，如果命中记3分，且停止射击；若第一次射击未命中，可以进行第二次射击，但目标已经在150米处，这时命中记2分，且停止射击；若第二次仍未命中，还可以进行第三次射击，此时目标已在200米处，若第三次命中则记1分，并停止射击；若三次都未命中，则记0分．已知射手甲在100米处击中目标的概率为

，他的命中率与目标的距离的平方成反比，且各次射击都是独立的．
（Ⅰ）求这名射手分别在第二次、第三次射击中命中目标的概率及三次射击中命中目标的概率；
（Ⅱ）设这名射手在比赛中得分数为ξ，求随机变量ξ的概率分布列和数学期望．

查看答案和解析>>

某种项目的射击比赛，开始时在距目标100米处射击，如果命中记3分，且停止射击，若第一次射击未命中，可以进行第二次射击，但目标已经在150米处，这时命中记2分，且停止射击；若第二次仍未命中，还可以进行第三次射击，此时目标已在200米处，若第三次命中则记1分，并停止射击；若三次都未命中，则记0分，已知射手甲在100m处击中目标的概率为

，他的命中率与目标的距离的平方成反比，且各次射击都是独立的．
（1）求这名射手在三次射击中命中目标的概率；
（2）求这名射手比赛中得分的均值．

查看答案和解析>>

（08年安徽信息交流文）（本小题满分12分）某种项目的射击比赛规定：开始时在距离目标100m处射击，如果命中记3分，同时停止射击；若第一次射击未命中目标，可以进行第二次射击，但目标已在150m远处，这时命中记2分，同时停止射击；若第二次射击仍未命中，可以进行第三次射击，但目标已在200m远处，这时命中记1分，同时停止射击。已知M射手在100m处命中目标的概率为，若他命中目标的概率与距离的平方成反比，且各次射击都是独立的。