题目列表(包括答案和解析)
（本小题满分10分）
在图1至图3中，直线MN与线段AB相交
于点O，∠1 = ∠2 = 45°．
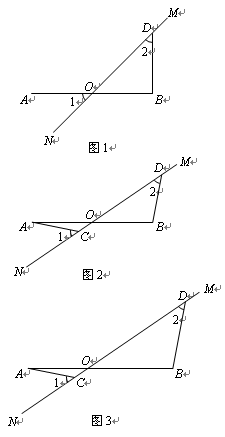
1.（1）如图1，若AO = OB，请写出AO与BD
的数量关系和位置关系；
2.（2）将图1中的MN绕点O顺时针旋转得到
图2，其中AO = OB．
求证：AC = BD，AC ⊥ BD；
3.（3）将图2中的OB拉长为AO的k倍得到
图3，求
的值．
（本小题满分10分）
元旦期间，商场中原价为 100元的某种商品经过两次连续降价后以每件81元出售，设这种商品每次降价的百分率相同，求这个百分率．
（本小题满分10分）
已知：如图，AD、BC是
的两条弦， 且
．求证：
．
（本小题满分10分）
△ABC中，AC=BC.以BC为直径作⊙O交AB于点D，交AC于点G.直线DF⊥AC，垂足为F,交CB的延长线于点E.
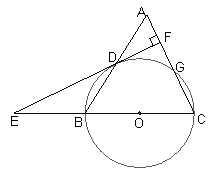
1.（1）判断直线EF与⊙O的位置关系，并说明理由；
2.（2）如果BC=10，AB=12，求CG的长.
（本小题满分10分）
在我们学习过的数学教科书中，有一个数学活动，其具体操作过程是：
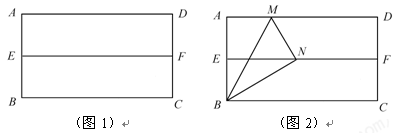
第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开（如图1）；
第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2）
请解答以下问题：
1.（1）如图2，若延长MN交BC于P，△BMP是什么三角形？请证明你的结论．
2.（2）在图2中，若AB=a，BC=b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合（1）中结论的三角形纸片BMP ？
一、选择题（每小题2分，共20分）
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
A
B
D
D
A
D
C
C
二、填空题（每小题3分，共24分）
11． 3 ； 12．12； 13．-3；
14．132； 15．
;
16．（0，2.5） 17．135° 18． 
三、解答题（本大题共8个小题；共76分）
19．解：原方程可化为
，……………………（4分）
∴
x＝2………………………………………（5分）
经检验，x＝2是原方程的根.………………………………………（7分）
20．解：⑴设蓝球个数为
个
-------1分
则由题意得
-------2分
答：蓝球有1个
--------3分
--------4分
---------5分
∴ 两次摸到都是白球的概率 =
=
----------7分
21. 解：过
作
，垂足是
，
则
．
点坐标是
．???????????????????????????????????????????????? 2分
过作
，垂足是
，
则
．
点坐标是
．??????????????????????????????????????????????? 4分
过作
，垂足是（如图），
则
，
．????????????????????? 6分
易知
，
，
．???????????????????????????? 8分
点
坐标是
．??????????????????????????????????????????????????????????????????????????????????????????????????? 9分
符合要求的点
有三个，其连线段分别是
（如图）．????????????????????????????? 10分
22．解：（1）在
中，
，
．????????????????????????????????????????????????????????????????????? 1分
在与
中，
；
∵
．
?????????????????????????????????????????????????????????????????????????????????????????????? 2分
．
和
都是等腰三角形．4分
（2）设
，则
，即
．??????????????????????????????????????? 4分
解得
（负根舍去）．?????????????????????????????????????????????????????? 6分
(3)
?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
23．解：（1）由
．???????????????????????????????????????????????????????? 2分
函数图象的顶点坐标为
，对称轴为直线
．?????????????????????????????????????? 4分
（2）如下右图．??????????????????????????????????????????????????????????????????????????????????????????????????????????? 7分
（3）从函数图象可以看出，从4月份开始新产品的销售累积利润盈利．??????????????????????? 8分
（4）
时，
，
时，
，
这个公司第6个月所获的利润是
万元．
10分
24．25．（1）判断：EN与MF相等 （或EN=MF），点F在直线NE上， ????? 3分
（说明：答对一个给2分）
（2）成立．??????????????????????????????? 4分
证明：
法一：连结DE，DF． ?????????????????????????? 5分
∵△ABC是等边三角形， ∴AB=AC=BC．
又∵D，E，F是三边的中点，
∴DE，DF，EF为三角形的中位线．∴DE=DF=EF，∠FDE=60°．
又∠MDF+∠FDN=60°， ∠NDE+∠FDN=60°，
∴∠MDF=∠NDE． ??????????????????????????? 7分
在△DMF和△DNE中，DF=DE，DM=DN， ∠MDF=∠NDE，
∴△DMF≌△DNE． ?????????????????????????? 8分
∴MF=NE．
?????????????????????????? 9分
法二：
延长EN，则EN过点F． ??????????????????????? 5分
∵△ABC是等边三角形， ∴AB=AC=BC．
又∵D，E，F是三边的中点， ∴EF=DF=BF．
∵∠BDM+∠MDF=60°， ∠FDN+∠MDF=60°，
∴∠BDM=∠FDN．???????????????????????????? 7分
又∵DM=DN， ∠ABM=∠DFN=60°，
∴△DBM≌△DFN．??????????????????????????? 8分
∴BM=FN．
∵BF=EF， ∴MF=EN．????????????????????????? 9分
（3）画出图形（连出线段NE），
|
时，设市场的日销售量
．
点
在图象上，
．
．即
．??????????????????????????????????????????????????????????????????????????????????????????? 2分
时，设市场的日销售量
．
在图象上，
．
．????????????????????????????????????????????????????????????????????????????????????????????????? 4分
．???????????????????????????????????????????? 6分
（天）时，市场的日销售量达到最大60万件；又由图2知，当
时，每件产品的日销售利润为
；
时，每件产品的日销售利润为
．
；
时，产品的日销售利润
最大等于2400万元．
时，产品的日销售利润
．
万元；
；
∴
，
（舍去）．………2分
．………………………………………………4分
．…………………6分
∽△
，
∴
，
．
．……………………8分 
． ………9分
，
．
．…………………………10分
④当8≤
．…………………………11分
．……………12分