
题目列表(包括答案和解析)
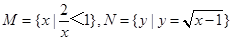 ,则
,则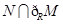 等于
等于 | A.(1,2) | B.[0,2] | C.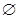 | D.[1,2] |
.已知集合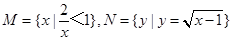 ,则
,则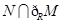 等于
等于
| A.(1,2) | B.[0,2] | C.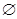 | D.[1,2] |
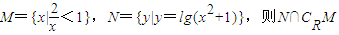 =( )
=( )设集合![]() =
=
A.(0,2) B.[-1,1] C.![]() D.
D.![]()
已知集合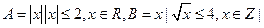 ,则
,则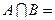
| A.(0,2) | B.[0,2] | C.|0,2| | D.|0,1,2| |
一、选择题:(共60分)
1.B 2.C 3.A 4.A 5.C 6.B 7.D 8.B 9.C 10.B 11.D 12.A
二、填空题;(本大题共5小题,每小题5分,共20分)
13.-3 14..files/image129.gif) 15.
15..files/image227.gif) 16.180
16.180
三、解答题:本大题有6小题,共70分,解答应写出文字说明,证明过程或演算步骤。
17.解:(1).files/image229.gif) 1分
1分
.files/image231.gif)
.files/image233.gif) 5分
5分
(2).files/image235.gif) 7分
7分
由余弦定理.files/image237.gif) 9分
9分
.files/image239.gif) 10分
10分
18. (1)记“该考生正确做出第.files/image241.gif) 道题”为事件
道题”为事件.files/image243.gif) 则
则.files/image245.gif) 由于每一道题能否被正确做出是相互独立的,所以这名考生首次做错一道题时,已正确做出了两掏题的概率为
由于每一道题能否被正确做出是相互独立的,所以这名考生首次做错一道题时,已正确做出了两掏题的概率为
.files/image247.gif)
(2)记“这名考生通过书面测试”为实践A,则这名考生至少正确做出3道题,即正确做出3道题或4道题,故.files/image249.gif) 6分
6分
19.解法一:
(1)在直平行六面体.files/image117.gif) -
-.files/image252.gif) 中,
中,
.files/image254.gif)
又.files/image256.gif)
.files/image258.jpg)
.files/image260.gif) 4分
4分
又.files/image262.gif) 6分
6分
(2)如图,连.files/image264.gif)
易证.files/image266.gif)
.files/image274.gif)
.files/image276.gif) 8分
8分
取.files/image278.gif) 中点
中点.files/image280.gif) ,连
,连.files/image282.gif) ,则
,则.files/image284.gif) ,
,
作.files/image286.gif) 由三垂线定理知:
由三垂线定理知:.files/image288.gif) ,则
,则.files/image290.gif) 是
是
在.files/image293.gif) 中,易求得
中,易求得.files/image295.gif)
.files/image297.gif) 中,
中,.files/image299.gif)
则二面角.files/image181.gif) 的大小为
的大小为.files/image302.gif) 12分
12分
解法二:
(1)以.files/image304.gif) 为坐标原点,射线
为坐标原点,射线.files/image306.gif) 为
为.files/image308.gif) 轴,建立如图所示坐标为
轴,建立如图所示坐标为.files/image310.gif) ,
,
依题设,.files/image312.gif)
.files/image314.gif)
.files/image316.gif)
.files/image318.gif)
又.files/image320.gif)
.files/image322.gif) 6分
6分
(2)由.files/image324.gif)
.files/image326.gif) 8分
8分
由(1)知平面.files/image328.gif) 的一个法向量为
的一个法向量为.files/image330.gif) =
=.files/image332.gif)
取.files/image334.gif) ,
,
.files/image336.gif)
.files/image338.jpg)
.files/image340.gif)
.files/image342.gif) 10分
10分
.files/image344.gif)
.files/image346.gif)
20.解:(1)由已知得:.files/image353.gif)
设数列.files/image107.gif) 的公比为
的公比为.files/image356.gif) ,由
,由.files/image358.gif) 4分
4分
可知.files/image360.gif)
由题意得.files/image362.gif) 》
》
故数列.files/image364.gif)
(2)由于.files/image366.gif)
.files/image368.gif)
.files/image370.gif)
.files/image372.gif)
21.解:(1)由已知得.files/image374.gif)
由.files/image376.gif)
.files/image378.gif)
当.files/image380.gif)
.files/image382.gif)
.files/image384.gif)
由题意得.files/image386.gif)
(2)由(1)知.files/image392.gif)
即.files/image394.gif)
又.files/image396.gif)
22.解:(1)设.files/image398.gif) 则
则.files/image400.gif)
.files/image402.gif) 得
得.files/image404.gif)
化简得.files/image406.gif)
法一:.files/image416.gif) 两点不可能关于
两点不可能关于.files/image308.gif) 轴对称,
轴对称,.files/image419.gif) 的斜率必存在
的斜率必存在
设直线.files/image224.gif) 的方程
的方程.files/image422.gif)
由.files/image424.gif)
.files/image426.gif)
.files/image428.gif)
且.files/image430.gif)
.files/image432.gif)
将.files/image434.gif) 代入化简得
代入化简得.files/image436.gif)
将.files/image438.gif) 代入
代入.files/image440.gif) 得
得.files/image442.gif) ,过定点
,过定点.files/image444.gif)
将.files/image446.gif) 入
入.files/image448.gif) 过定点(1,2)即为A点,舍去
过定点(1,2)即为A点,舍去
法二:设.files/image452.gif)
同理.files/image454.gif)
设直线.files/image224.gif) 的方程为
的方程为.files/image457.gif)
得.files/image459.gif)
.files/image461.gif) 直线
直线.files/image224.gif) 的方程为
的方程为.files/image464.gif)
即.files/image466.gif) 直线
直线.files/image224.gif) 过定点(-1,-2)
过定点(-1,-2)
22.解:(1)由.files/image469.gif)
于是.files/image471.gif)
即.files/image473.gif)
有.files/image475.gif)
.files/image477.gif)
(2)由(1)得.files/image479.gif)
而.files/image481.gif)
.files/image483.gif)
=.files/image485.gif)
=.files/image487.gif)
当.files/image489.gif)
故命题得证
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com