
题目列表(包括答案和解析)
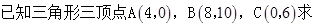
 ;
; 。
。。】若函数![]() 在区间
在区间![]() 上的图象为连续不断的一条曲线,
上的图象为连续不断的一条曲线,
则下列说法正确的是( )
A.若![]() ,不存在实数
,不存在实数![]() 使得
使得![]() ;
;
B.若![]() ,存在且只存在一个实数
,存在且只存在一个实数![]() 使得
使得![]() ;
;
C.若![]() ,有可能存在实数
,有可能存在实数![]() 使得
使得![]() ;
;
D.若![]() ,有可能不存在实数
,有可能不存在实数![]() 使得
使得![]() ;
;
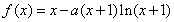 。
。
(Ⅰ)求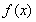 的极值点;
的极值点;
(Ⅱ)当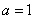 时,若方程
时,若方程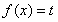 在
在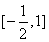 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围;
(Ⅲ)证明:当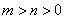 时,
时, 。
。
(14分)。函数y=Asin(ωx+φ)(A>0,ω>0)在x∈(0,7π)内取到一个
最大值和一个最小值,且当x=π时,y有最大值3,当x=6π时,y有最小值-3.
(1)求此函数解析式;
(2)是否存在实数ω,满足Asin(ω +φ)>Asin(ω
+φ)>Asin(ω +φ)?若存在,求出m.若不存在,说明理由.
+φ)?若存在,求出m.若不存在,说明理由.
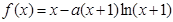 。
。
(Ⅰ)求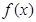 的极值点;
的极值点;
(Ⅱ)当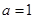 时,若方程
时,若方程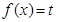 在
在 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围;
(Ⅲ)证明:当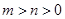 时,
时,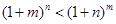 。
。
一、填空题
1.  2.
2.
 3.156
4. -
3.156
4. - 5.
5. 
6. 7.
7. 8.(理)
8.(理) (文)
(文) 9.0
9.0
10. 11.(理)
11.(理) (文)
(文)
二、选择题
12.C 13.B 14.(理)C (文)B 15.B
三、解答题
16. 【解】(1)由已知: , (2分)
, (2分)
即 , (4分)
, (4分)
∴ ,故
,故 。
(6分)
。
(6分)
(2)由 ,得
,得 , (8分)
, (8分)
∴ ,
, 。 (10分)
。 (10分)
故 。
(12分)
。
(12分)
17.【解】
(理)设三次事件依次为 ,命中率分别为
,命中率分别为 ,
,
(1)令 ,则
,则 ,∴
,∴ ,
, ,
, 。 (6分)
。 (6分)
(2) 。 (13分)
。 (13分)
(文)抛物线 的准线是
的准线是 ,
(3分)
,
(3分)
双曲线 的两条渐近线是
的两条渐近线是 。 (6分)
。 (6分)
三条线为成得三角形区域的顶点为 ,
, ,
, ,(10分)
,(10分)
当 时,
时, 。
(13分)
。
(13分)
18.【解】(1) ,
, 。(4分)
。(4分)
(2)令 ,
, ,
,
 ,(8分)
,(8分)
即三位市民各获得140、100和110元折扣。(10分)
(3) (元)。(16分)
(元)。(16分)
19.【解】(1)直线 的法向量
的法向量 ,
, 的方程:
的方程: ,
,
即为 ;…(2分)
;…(2分)
直线 的法向量
的法向量 ,
, 的方程:
的方程: ,
,
即为 。 (4分)
。 (4分)
(2) 。 (6分)
。 (6分)
设点 的坐标为
的坐标为 ,由
,由 ,得
,得 。(8分)
。(8分)
由椭圆的定义的知存在两个定点 ,使得
,使得 恒为定值4。
恒为定值4。
此时两个定点 为椭圆的两个焦点。(10分)
为椭圆的两个焦点。(10分)
(3)设 ,
, ,则
,则 ,
, ,
,
由 ,得
,得 。(12分)
。(12分)
 ;
;
当且仅当 或
或 时,
时, 取最小值
取最小值 。(14分)
。(14分)
 ,故
,故 与
与 平行。(16分)
平行。(16分)
20.【解】(1)由 ,得
,得 。由
。由 ,得第二行的公差
,得第二行的公差 ,
, ,∴
,∴ 。(2分)
。(2分)
由 ,
, ,得
,得 ,∴
,∴ 。(4分)
。(4分)
(2) ;(6分)
;(6分)
 。(10分)
。(10分)
(3) ,
, , 两式相减,得
, 两式相减,得 ,
, 。(12分)当
。(12分)当 时,
时, 。(13分)
。(13分)
① 时,
时, 显然能被21整除;(14分)
显然能被21整除;(14分)
②假设 时,
时, 能被21整除,当
能被21整除,当 时,
时,
 能被21整除。结论也成立。(17分)
能被21整除。结论也成立。(17分)
由①、②可知,当 是3的倍数时,
是3的倍数时, 能被21整除。(18分)
能被21整除。(18分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com