
题目列表(包括答案和解析)
 某实验小组在利用单摆测定当地重力加速度的实验中:
某实验小组在利用单摆测定当地重力加速度的实验中:| t | n |
某实验小组在利用单摆测定当地重力加速度的实验中: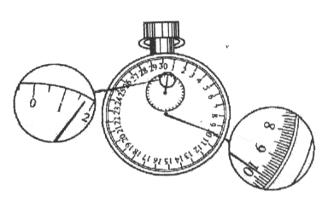
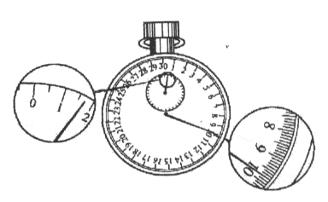
(1)用摆长L和周期T计算重力加速度的公式是g= ,如果测定了40次全振动的时间为如图中停表所示,则停表读数是 。
(2)小组成员在实验过程中,有如下做法,其中正确的是 。
| A.用夹子把单摆摆线的上端固定在铁架台上 |
| B.把单摆从平衡位置拉开一定角度,并在释放摆球的同时开始计时 |
C.测量摆球通过最低点n次的时间t,则单摆周期为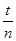 |
| D.用悬线长度加摆球直径作为摆长,计算得到的重力加速度值偏大 |
某实验小组在利用单摆测定当地重力加速度的实验中:
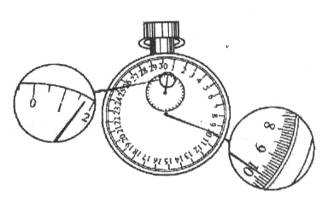
(1)用摆长L和周期T计算重力加速度的公式是g= ,如果测定了40次全振动的时间为如图中停表所示,则停表读数是 。
(2)小组成员在实验过程中,有如下做法,其中正确的是 。
A. 用夹子把单摆摆线的上端固定在铁架台上
B. 把单摆从平衡位置拉开一定角度,并在释放摆球的同时开始计时
C. 测量摆球通过最低点n次的时间t,则单摆周期为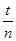
D. 用悬线长度加摆球直径作为摆长,计算得到的重力加速度值偏大
E. 选择质量较小的摆球,测得的重力加速度值较小

| A.用夹子把单摆摆线的上端固定在铁架台上 |
| B.把单摆从平衡位置拉开一定角度,并在释放摆球的同时开始计时 |
C.测量摆球通过最低点n次的时间t,则单摆周期为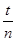 |
| D.用悬线长度加摆球直径作为摆长,计算得到的重力加速度值偏大 |
一、1、AB 2、AD3、A 4、C5、D 6、C 7、C 8、AC
二、实验题:(18分)将答案填在题目的空白处,或者要画图连线。
 9、(6分)(1)0。48;0。40(2)②(3)mgs;(4)①;(5)增加的动能;摩擦、定滑轮转动。[只要言之有理就给分。比如,若回答减少的重力势能可能偏小,原因是数字计时读出遮光条通过光电门的时间
9、(6分)(1)0。48;0。40(2)②(3)mgs;(4)①;(5)增加的动能;摩擦、定滑轮转动。[只要言之有理就给分。比如,若回答减少的重力势能可能偏小,原因是数字计时读出遮光条通过光电门的时间 t偏小而造成的](除5以外各步是1分(5)是2分)
t偏小而造成的](除5以外各步是1分(5)是2分)
10、(12分)①C (3分)
②电路如图所示。(5分)
③ ,(2分)
,(2分) 为电压表读数,
为电压表读数, 为电压表内阻。(2分)
为电压表内阻。(2分)
三、本大题共三小题共计54分.解答时请写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分.有数值计算的题.答案中必须明确写出数值和单位
11、(16分)受力分析如图,据牛顿第二定律有

 ①
①
减速上升250m与加速下降250m互逆
据题意 ②
②
 ③
③
代入数据可得
 ④
④
 ⑤
⑤
设计师应设计发射速度
同时数码点火控制时间应设定
评分参考:①②③式分别得4分,④④式分别得2分
12、(18分)(1)在圆形磁场中做匀速圆周运动,
洛仑兹力提供向心力 ……………………………… 2分
……………………………… 2分
得 ……………………………………………………… 1分
……………………………………………………… 1分
(2)根据题意粒子恰好不能从O3射出的条件为 ………… 2分
………… 2分
PQ其匀速运动时, ………………………………… 2分
………………………………… 2分
由③④得 …………………………………………… 1分
…………………………………………… 1分
(3)导体棒匀速运动时,速度大小为 ………… 1分
………… 1分
代入③中得: …………………………………………… 1分
…………………………………………… 1分
由能量守恒:
解得 ……………………………………
2分
……………………………………
2分
(4)在圆形磁场内的运动时间为t1
 ……………………………………………
2分
……………………………………………
2分
在电场中往返运动的时间为t2
由 ……………………………………………………… 2分
……………………………………………………… 2分
 ……………………………………………………………… 1分
……………………………………………………………… 1分
故 …………………………………… 1分
…………………………………… 1分
13、(20分)(1)粒子进入电容器,其加速度a= ……………① (1分)
……………① (1分)
假设能在 时间以内穿过电容器,则有
时间以内穿过电容器,则有 at2=D……………② (1分)
at2=D……………② (1分)
由以上两式并代入数据得:t= s……………………………………(3分)
s……………………………………(3分)
t< 符合假设,故粒子经7.1×10-6s到达磁场。……………………………(1分)
符合假设,故粒子经7.1×10-6s到达磁场。……………………………(1分)
(2)设粒子到达磁场时的速率为v
由动能定理得:qU= ……………③ (2分)
……………③ (2分)
粒子进入磁场在洛仑兹力作用下做匀速圆周运动,其半径为R,有
 qvB=
qvB= ……………④ (2分)
……………④ (2分)
粒子运动轨迹如图,由几何知识有:
(R-L)2+d2=R2……………⑤ (2分)
根据③④⑤式得粒子向上偏移的距离
L= m=4.1×10-
m=4.1×10-
(3)如果粒子在磁场中的轨迹恰好与右边界相切,则半径R0=d,对应速度为v0
设在电场中先加速位移x,后减速位移D-x
由动能定理: …………⑦ (2分)
…………⑦ (2分)
加速位移x需要时间为t,x= …………⑧ (2分)
…………⑧ (2分)
由④⑥⑦⑧得 t= s …………⑨ (2分)
s …………⑨ (2分)
故需在0―( -t)内进入电容器,即在0―3.9×10-7s进入。…………(1分)
-t)内进入电容器,即在0―3.9×10-7s进入。…………(1分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com