
题目列表(包括答案和解析)
| 3x |
| 4 |
| x3 |
| 3 |
| 1 |
| 2 |
| 3x |
| 4 |
| x3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| sinx |
| 4 |
设M是由满足下列条件的函数![]() 构成的集合:“①方程
构成的集合:“①方程![]()
![]() 有实数根;②函数
有实数根;②函数![]() 的导数
的导数![]() 满足
满足![]() .”
.”
(I)判断函数![]() 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中的元素![]() 具有下面的性质:若
具有下面的性质:若![]() 的定义域为D,则对于任意
的定义域为D,则对于任意
[m,n]![]() D,都存在
D,都存在![]()
![]() [m,n],使得等式
[m,n],使得等式![]() 成立”,
成立”,
试用这一性质证明:方程![]() 只有一个实数根;
只有一个实数根;
(III)设![]() 是方程
是方程![]() 的实数根,求证:对于
的实数根,求证:对于![]() 定义域中任意的
定义域中任意的![]() .
.
 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;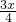 +
+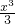 (0≤x<
(0≤x< )是集合M中的元素;
)是集合M中的元素;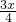 +
+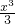 (0≤x
(0≤x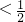 )具有下面的性质:对于任意[m,n]⊆[0,
)具有下面的性质:对于任意[m,n]⊆[0, ),都存在xo∈(m,n),使得等式f(n)-f(m)=(n-m)f′(xo)成立.
),都存在xo∈(m,n),使得等式f(n)-f(m)=(n-m)f′(xo)成立.一、选择题(本大题共8小题,每小题5分,共40分.)
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
答案
D
B
A
C
D
C
B
C
二、填空题(本大题共6小题,每小题5分.有两空的小题,第一空3分,第二空2分,共30分)
(9) .files\image066.gif) (10)
(10) .files\image209.gif) 或
或.files\image211.gif) (11)
(11)
.files\image213.gif)
(12) .files\image215.gif) ,
, .files\image217.gif) (13)
(13).files\image219.gif) (14)4,8
(14)4,8
三、解答题(本大题共6小题,共80分.)
(15) (共12 分)
解:(I).files\image221.gif)
.files\image133.gif) ,
,.files\image135.gif) ,
,
.files\image223.gif)
.files\image129.gif)
.files\image131.gif) =
=.files\image225.gif) ?
?.files\image227.gif)
.files\image229.gif) 2分
2分
.files\image231.gif) 4分
4分
.files\image232.gif)
.files\image139.gif) =
= .files\image234.gif) . 5分
. 5分
又.files\image236.gif)
.files\image238.gif)
.files\image240.gif) 6分
6分
.files\image232.gif) 函数
函数.files\image141.gif) 的最大值为
的最大值为.files\image242.gif) .
7分
.
7分
当且仅当.files\image244.gif) (
(.files\image246.gif) Z)时,函数
Z)时,函数.files\image141.gif) 取得最大值为
取得最大值为.files\image242.gif) .
.
(II)由.files\image248.gif) (
(.files\image246.gif) Z),
9分
Z),
9分
得.files\image250.gif) (
(.files\image246.gif) Z).
11分
Z).
11分
.files\image232.gif) 函数
函数.files\image141.gif) 的单调递增区间为[
的单调递增区间为[.files\image252.gif) ](
](.files\image246.gif) Z). 12分
Z). 12分
(16) (共14分)
解法一:(I)证明:连结A1D,在正方体AC1中, ∵A1B1^平面A1ADD1,
\ A1D是PD在平面A1ADD1 内的射影. 2分
在正方形A1ADD1中, A1D^ AD1, \ PD⊥AD1. 4分
解(II) 取.files\image255.gif) 中点
中点.files\image257.gif) ,连结
,连结.files\image259.gif) ,
,.files\image261.gif) ,则
,则.files\image259.gif) //
//.files\image263.gif) .
.
.files\image221.gif)
.files\image266.gif) 平面
平面.files\image268.gif) ,∴
,∴.files\image259.gif)
.files\image270.gif) 平面
平面.files\image268.gif) .
.
∴.files\image261.gif) 为
为.files\image272.gif) 在平面
在平面.files\image268.gif) 内的射影.
内的射影.
则.files\image274.gif) 为CP与平面D1DCC1所成的角.
7分
为CP与平面D1DCC1所成的角.
7分
在.files\image276.gif) 中,
中,.files\image278.gif)
.files\image280.jpg) ∴
∴.files\image272.gif) 与平面D1DCC1所成的角的正弦值为
与平面D1DCC1所成的角的正弦值为.files\image283.gif) . 9分
. 9分
(III)在正方体AC1中,.files\image285.gif) ∥
∥.files\image287.gif) .
.
.files\image289.gif) 平面
平面.files\image291.gif) 内,
内,
∴.files\image287.gif) ∥平面
∥平面.files\image291.gif) .
.
∴点.files\image294.gif) 到平面
到平面.files\image291.gif) 的距离与点C1到平面
的距离与点C1到平面.files\image291.gif) 的距离相等.
的距离相等.
又.files\image285.gif)
.files\image270.gif) 平面
平面.files\image299.gif) ,
,.files\image301.gif) 面
面.files\image303.gif) ,
,
∴平面.files\image291.gif)
.files\image270.gif) 平面
平面.files\image299.gif) .
.
又平面.files\image303.gif)
.files\image307.gif) 平面
平面.files\image309.gif) ,
,
过C1作C1H.files\image311.gif) 于H,则C1H
于H,则C1H.files\image270.gif) 平面
平面.files\image291.gif) .
.
∴C1.files\image314.gif) 的长为点C1到平面
的长为点C1到平面.files\image291.gif) 的距离.
12分
的距离.
12分
连结C1.files\image317.gif) ,并在
,并在.files\image319.gif) 上取点
上取点.files\image321.gif) ,使
,使.files\image323.gif) //
//.files\image325.gif) .
.
在.files\image327.gif) 中,
中,.files\image329.gif) ,得
,得.files\image331.gif) .
.
∴点.files\image294.gif) 到平面
到平面.files\image291.gif) 的距离为
的距离为.files\image334.gif) .
14分
.
14分
解法二:如图,以D为坐标原点,建立空间直角坐标系.files\image336.gif) .
.
由题设知正方体棱长为4,则.files\image338.gif) 、
、.files\image340.gif) 、
、
.files\image342.gif) 、
、.files\image344.gif) 、
、.files\image346.gif) 、
、.files\image348.gif) .
1分
.
1分
(I)设.files\image350.gif) ,
,.files\image352.gif) .
. .files\image354.gif) 3分
3分
.files\image356.gif) ,
, .files\image358.gif) .
4分
.
4分
.files\image360.jpg) (II)由题设可得,
(II)由题设可得,.files\image362.gif) , 故
, 故.files\image364.gif) .
.
.files\image366.gif) ,
, .files\image368.gif) 是平面
是平面
.files\image268.gif) 的法向量.
7分
的法向量.
7分
.files\image371.gif) .
8分
.
8分
∴.files\image272.gif) 与平面D1DCC1所成角的正弦值为
与平面D1DCC1所成角的正弦值为.files\image283.gif) .
9分
.
9分
(III).files\image373.gif) ,设平面D1DP的法向量
,设平面D1DP的法向量.files\image375.gif) ,
,
∵.files\image377.gif)
.files\image379.gif) .
.
则.files\image381.gif) ,即
,即.files\image383.gif) 令
令.files\image385.gif) ,则
,则.files\image387.gif)
.files\image223.gif)
.files\image390.gif) .
12分
.
12分
.files\image223.gif) 点C到平面D1DP的距离为
点C到平面D1DP的距离为.files\image392.gif) .
14分
.
14分
(17)(共13分)
解(I)设事件“某人参加A种竞猜活动只获得一个福娃奖品”为事件M, 1分
依题意,答对一题的概率为.files\image394.gif) ,则
,则
P(M)=.files\image396.gif) 3分
3分
=.files\image398.gif) .
4分
.
4分
(II)依题意,某人参加B种竞猜活动,结束时答题数.files\image152.gif) =1,2,…,6,
5分
=1,2,…,6,
5分
则.files\image400.gif) ,
,.files\image402.gif) ,
,.files\image404.gif) ,
,.files\image406.gif) ,
,
.files\image408.gif) ,
,.files\image410.gif) .
11分
.
11分
所以,.files\image152.gif) 的分布列是
的分布列是
.files\image152.gif)
1
2
3
4
5
6
P
.files\image394.gif)
.files\image412.gif)
.files\image414.gif)
.files\image416.gif)
.files\image418.gif)
.files\image420.gif)
.files\image422.gif)
设.files\image424.gif) ,
,
则.files\image426.gif)
∴.files\image428.gif)
.files\image430.gif)
.files\image432.gif) ,
,
∴ E.files\image152.gif) =
=.files\image430.gif)
.files\image434.gif) =
=.files\image436.gif) .
13分
.
13分
答:某人参加A种竞猜活动只获得一个福娃奖品的概率为.files\image438.gif) ;某人参加B种竞猜活动,结束时答题数为
;某人参加B种竞猜活动,结束时答题数为.files\image152.gif) ,E
,E.files\image152.gif) 为
为.files\image440.gif) .
.
.files\image442.gif)
(18)(本小题共13分)
解;如图,建立直角坐标系,依题意:设椭圆方
程为.files\image444.gif) (a>b>0), 1分
(a>b>0), 1分
(I)依题意:.files\image446.gif) 4分
4分
.files\image221.gif) 椭圆M的离心率大于0.7,所以
椭圆M的离心率大于0.7,所以.files\image449.gif) .
.
.files\image223.gif) 椭圆方程为
椭圆方程为.files\image452.gif) .
6分
.
6分
(II)因为直线l过原点与椭圆交于点.files\image160.gif) ,设椭圆M的左焦点为
,设椭圆M的左焦点为.files\image455.gif) .
.
由对称性可知,四边形.files\image457.gif) 是平行四边形.
是平行四边形.
.files\image223.gif)
.files\image166.gif) 的面积等于
的面积等于.files\image460.gif) 的面积.
8分
的面积.
8分
∵
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com