
题目列表(包括答案和解析)
(本小题满分12分)二次函数![]() 的图象经过三点
的图象经过三点![]() .
.![]()
(1)求函数![]() 的解析式(2)求函数
的解析式(2)求函数![]() 在区间
在区间![]() 上的最大值和最小值
上的最大值和最小值
(本小题满分12分)已知等比数列{an}中,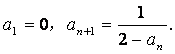
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设数列{an}的前n项和为Sn,证明:![]() ;
;
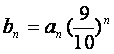 ,证明:对任意的正整数n、m,均有
,证明:对任意的正整数n、m,均有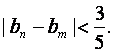
(本小题满分12分)已知函数![]() ,其中a为常数.
,其中a为常数.
(Ⅰ)若当![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
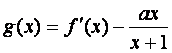 的单调区间.
的单调区间.(本小题满分12分)
甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为![]() ,乙投篮命中的概率为
,乙投篮命中的概率为![]()
(Ⅰ)求甲至多命中2个且乙至少命中2个的概率;
(Ⅱ)若规定每投篮一次命中得3分,未命中得-1分,求乙所得分数η的概率分布和数学期望.(本小题满分12分)已知![]() 是椭圆
是椭圆![]() 的两个焦点,O为坐标原点,点
的两个焦点,O为坐标原点,点![]() 在椭圆上,且
在椭圆上,且![]() ,圆O是以
,圆O是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与圆O相切,并且与椭圆交于不同的两点A、B.
与圆O相切,并且与椭圆交于不同的两点A、B.
(1)求椭圆的标准方程;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)当![]() 时,求弦长|AB|的取值范围.
时,求弦长|AB|的取值范围.
一、选择题(每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
B
B
A
D
C
D
B
C
A
D
二、填空题(每小题4分,共16分)
13、120; 14、20; 15、 ;16、2.
;16、2.
三、解答题
17、解:(Ⅰ)由正弦定理得 ,
,
即 ……2分
……2分
得 ,因为
,因为 ,所以
,所以 ,得
,得 ……3分,因为
……3分,因为 ,
,
所以 ,又
,又 为三角形的内角,所以
为三角形的内角,所以 ……2分
……2分
(Ⅱ) ,由
,由 及
及 得
得 ……2分
……2分

 ,
,
又 ,所以当
,所以当 时,
时, 取最大值
取最大值 ……3分
……3分
18、解:(Ⅰ)设公差为 ,由
,由 ,得
,得 ,
,
 ,因为数列{
,因为数列{ }的各项均为正数,
}的各项均为正数,
所以得 ……3分
又
……3分
又 ,所以
,所以 ……2分
……2分
由 ,
, 得
得 ……1分
……1分
(Ⅱ)由(Ⅰ)得 ……2分
……2分
于是
 ……4分
……4分
 19、(Ⅰ)如图,连结
19、(Ⅰ)如图,连结 ,因为
,因为 、
、
分别是棱 、
、 的中点,
的中点,
所以 ……2分
……2分
因为 平面
平面 ,
, ,
, 不在平面
不在平面
 内,所以
内,所以 平面
平面 ……3分
……3分
(Ⅱ)解:因为 平面
平面 ,
,
所以 ,因为
,因为 是直角梯形,
是直角梯形,
且 ,所以
,所以 ,又
,又 ,所以
,所以 平面
平面 ,即
,即 是三棱锥
是三棱锥 的高 ……4分
的高 ……4分
因为 是棱
是棱 的中点,所以
的中点,所以
 ,
,
于是三棱锥 的体积
的体积 ……3分
……3分
20、解:从5名同学 、
、 、
、 、
、 、
、 中选出3名同学的基本事件空间为:
中选出3名同学的基本事件空间为:

 ,共含有10个基本事件 ……3分
,共含有10个基本事件 ……3分
(Ⅰ)设事件 为“
为“ 同学被选取”,则事件
同学被选取”,则事件 包含6个基本事件,
包含6个基本事件,
事件 发生的概率为
发生的概率为 ……3分
……3分
(Ⅱ)设事件 为“
为“ 同学和
同学和 同学都被选取”,则事件
同学都被选取”,则事件 包含3个基本事件,
包含3个基本事件,
事件 发生的概率为
发生的概率为 ……3分
……3分
(Ⅲ)设事件 为“
为“ 同学和
同学和 同学中至少有一个被选取”,则事件
同学中至少有一个被选取”,则事件 包含9个基本事件,事件
包含9个基本事件,事件 发生的概率为
发生的概率为 ……3分
……3分
21、解:(Ⅰ)由 得
得 ……2分
……2分
由点 (
( ,0),
,0), (0,
(0, )知直线
)知直线 的方程为
的方程为 ,
,
于是可得直线 的方程为
的方程为 ……2分
……2分
因此 ,得
,得 ,
, ,
, ,
,
所以椭圆 的方程为
的方程为 ……2分
……2分
(Ⅱ)由(Ⅰ)知 、
、 的坐标依次为(2,0)、
的坐标依次为(2,0)、 ,
,
因为直线 经过点
经过点 ,所以
,所以 ,得
,得 ,
,
即得直线 的方程为
的方程为 ……2分
……2分
因为 ,所以
,所以 ,即
,即 ……1分
……1分
设 的坐标为
的坐标为 ,则
,则
得 ,即直线
,即直线 的斜率为4 ……2分
的斜率为4 ……2分
又点 的坐标为
的坐标为 ,因此直线
,因此直线 的方程为
的方程为 ……1分
……1分
22、解:(Ⅰ) ,因为
,因为 在
在 时取得极值,
时取得极值,
所以 是方程
是方程 的根,即
的根,即 ……2分
……2分
得 ,又因为
,又因为 ,
,
所以 的取值范围是
的取值范围是 ……2分
……2分
(Ⅱ)当 时,
时, ,
, ,
,
因为 ,当
,当 时,
时, ,
, 在
在 内单调递减……2分
内单调递减……2分
当 时,
时, ,令
,令 解得
解得
 或
或 ,令
,令 ,解得
,解得 ,
,
于是当 时,
时, 在
在 内单调递增,
内单调递增,
在 内单调递减 ……2分
内单调递减 ……2分
(Ⅲ)因为函数 在
在 时有极值
时有极值 ,所以有
,所以有 ,
,
消去 得
得 ,解之得
,解之得 或
或 ,又
,又 ,所以取
,所以取 ,
,
此时 ……2分
……2分
因此 ,
, ,
,
可得 当
当 时取极大值
时取极大值 ,
,
 当
当 时取极小值
时取极小值 ……2分
……2分
如图,方程 有三个不相等的实数根,等价于直线
有三个不相等的实数根,等价于直线 与曲线
与曲线
 有三个不同的交点,由图象得
有三个不同的交点,由图象得 ……2分
……2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com