
题目列表(包括答案和解析)
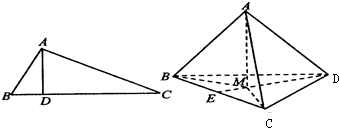 如图,在△ABC中,AB⊥AC,若AD⊥BC,则AB2=BD•BC;类似地有命题:在三棱锥A-BCD中,AD⊥面ABC,若A点在BCD内的射影为M,则有
如图,在△ABC中,AB⊥AC,若AD⊥BC,则AB2=BD•BC;类似地有命题:在三棱锥A-BCD中,AD⊥面ABC,若A点在BCD内的射影为M,则有| S | 2 △ABC |
如图,四棱锥V-ABCD中,∠BCD=∠BAD=90°,又∠BCV=∠BAV=90°,
求证:VD⊥AC;
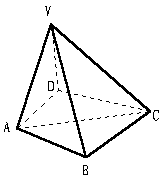
在平面内,余弦定理给出了三角形的三条边与其中一个角的关系,如:  ,把四面体V-BCD与三角形作类比,设二面角V-BC-D,V-CD-B, V-BD-C,C-VB-D,B-VC-D,B-VD-C的大小依次为
,把四面体V-BCD与三角形作类比,设二面角V-BC-D,V-CD-B, V-BD-C,C-VB-D,B-VC-D,B-VD-C的大小依次为 我们可以得到“四面体的余弦定理”:_____________________.(只需写出一个关系式)
我们可以得到“四面体的余弦定理”:_____________________.(只需写出一个关系式)
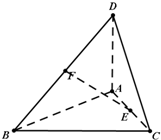 如图,三棱锥A-BCD中,AB⊥AD,AC⊥AD,∠BAC=θ(0<θ≤
如图,三棱锥A-BCD中,AB⊥AD,AC⊥AD,∠BAC=θ(0<θ≤| π | 2 |
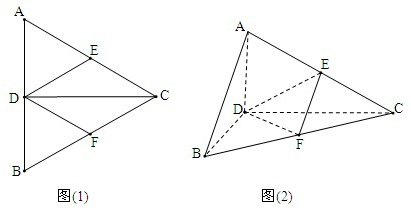 如图(1)所示,正△ABC的边长为2a,CD是AB边上的高,E,F分别是AC,BC的中点.现将△ABC沿CD翻折,使翻折后平面ACD⊥平面BCD(如图(2)),
如图(1)所示,正△ABC的边长为2a,CD是AB边上的高,E,F分别是AC,BC的中点.现将△ABC沿CD翻折,使翻折后平面ACD⊥平面BCD(如图(2)),湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com