
题目列表(包括答案和解析)
在平面直角坐标系中,圆M∶(x-1)2+(y-1)2=5在点A(3,2)处的切线方程可如下求解:设P(x,y)为切线上任一点,则由向量方法可得切线方程为:2x+y-8=0,类似地,在空间直角坐标系中,球M∶(x-1)2+(y-1)2+(z-1)2=6在点A(3,2,2)处的切面方程为________.
 =
= ,
, =
= ,
, =
= .试用向量法解下列问题:
.试用向量法解下列问题:
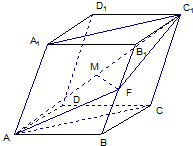 已知四棱柱ABCD-A1B1C1D1中的底面是菱形,且∠DAB=∠A1AB=∠A1AD=60°,AD=1,AA1=a,F为棱BB的中点,M为线段AC的中点.设
已知四棱柱ABCD-A1B1C1D1中的底面是菱形,且∠DAB=∠A1AB=∠A1AD=60°,AD=1,AA1=a,F为棱BB的中点,M为线段AC的中点.设| AB |
| e1 |
| AD |
| e2 |
| AA1 |
| e3 |
如图,在正方体 中,
中,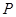 是棱
是棱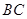 的中点,
的中点,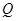 在棱
在棱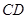 上.
上.
且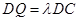 ,若二面角
,若二面角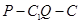 的余弦值为
的余弦值为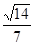 ,求实数
,求实数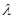 的值.
的值.
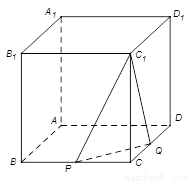
【解析】以A点为坐标原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,设正方体的棱长为4,分别求出平面C1PQ法向量和面C1PQ的一个法向量,然后求出两法向量的夹角,建立等量关系,即可求出参数λ的值.
(本题满分18分,其中第1小题5分,第2小题5分,第3小题8分)
在平面直角坐标系中,已知![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() 且
且![]() .设
.设![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求方程
,求方程![]() 在区间
在区间![]() 内的解集;
内的解集;
(2)若点![]() 是过点
是过点![]() 且法向量为
且法向量为![]() 的直线
的直线![]() 上的动点.当
上的动点.当![]() 时,设函数
时,设函数![]() 的值域为集合
的值域为集合![]() ,不等式
,不等式![]() 的解集为集合
的解集为集合![]() . 若
. 若![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)根据本题条件我们可以知道,函数![]() 的性质取决于变量
的性质取决于变量![]() 、
、![]() 和
和![]() 的值. 当
的值. 当![]() 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数![]() 满足“图像关于点
满足“图像关于点![]() 对称,且在
对称,且在![]() 处
处![]() 取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com