
题目列表(包括答案和解析)
平面内与直线平行的非零向量称为直线的方向向量,与直线的方向向量垂直的非零向量称为直线的法向量.在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点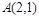 且法向量为
且法向量为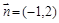 的直线(点法式)方程为
的直线(点法式)方程为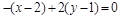 ,化简后得
,化简后得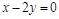 .则在空间直角坐标系中,平面经过点
.则在空间直角坐标系中,平面经过点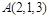 ,且法向量为
,且法向量为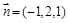 的平面(点法式)方程化简后的结果为 .
的平面(点法式)方程化简后的结果为 .
已知AO为平面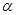 的一条斜线,O为斜足,OB为OA在平面
的一条斜线,O为斜足,OB为OA在平面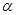 内的射影,直线OC在平面
内的射影,直线OC在平面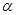 内,且
内,且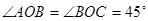 ,则
,则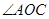 的大小为( )
的大小为( )
(A)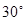 (B)
(B)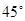 (C)
(C)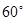 (D)
(D)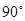
| n |
| n |
(08年莆田四中一模理)有以下几个命题:
①由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到
个单位长度可以得到![]() 的图象;
的图象;
②若![]() ,则使
,则使![]() 取得最大值和最小值的最优解都有无数多个;
取得最大值和最小值的最优解都有无数多个;
③若![]() 为一平面内两非零向量,则
为一平面内两非零向量,则![]() 是
是![]() 的充要条件;
的充要条件;
④过空间上任意一点有且只有一个平面与两条异面直线都平行。
⑤若椭圆的左、右焦点分别为![]() ,
,![]() 是该椭圆上的任意一点,则点
是该椭圆上的任意一点,则点![]() 关于
关于![]() 的外角平分线的对称点
的外角平分线的对称点![]() 的轨迹是圆。其中真命题的序号为 .(写出所有真命题的序号)
的轨迹是圆。其中真命题的序号为 .(写出所有真命题的序号)
| n |
| n |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com