
题目列表(包括答案和解析)
求证:一个三角形中,至少有一个内角不小于 ,用反证法证明时的假设为“三角形的 ”.
,用反证法证明时的假设为“三角形的 ”.
求证:一个三角形中,至少有一个内角不小于![]() ,用反证法证明时的假设为“三角形的 ”.
,用反证法证明时的假设为“三角形的 ”.
设
 ,求证:
,求证: .
.设
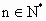 ,求证:
,求证: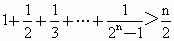 .
.设
 ,
,
求证:
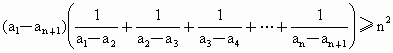 .
.说明:
一、本解答给出一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题
的主要考查内容比照评分标准制订相应的评分细则.
二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的
内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如
果后续部分的解答有较严重的错误,就不再给分.
三、解答右端所注分数,表示考生正确做到这一步应得累加分.
四、只给整数分数,选择题和填空题不给中间分数.
一、选择题(每小题5分,满分60分)
1.C 2.D 3.D 4.C 5.B 6.B 7.A 8.D 9.B 10.B 11.A 12.C
简答与提示:
1..files/image210.gif) ,故选C.
,故选C.
2.∵.files/image212.gif)
∴.files/image214.gif) ,故选D.
,故选D.
3.因为四个命题均有线在面内的可能,所以均不正确,故选D.
4..files/image216.gif) ,故选C.
,故选C.
5.利用叠加法及等比数列求和公式,可求得.files/image218.gif) ,故选B.
,故选B.
6.以.files/image220.gif) 为直径的圆与圆
为直径的圆与圆.files/image055.gif) 的公共弦即为所求,直线方程为
的公共弦即为所求,直线方程为.files/image059.gif) ,故
,故
选B.
7..files/image224.gif) ,将
,将.files/image065.gif) 的图象先向左平移
的图象先向左平移.files/image069.gif) 个单位得到
个单位得到
.files/image228.gif) 的图象,再沿
的图象,再沿.files/image071.gif) 轴将横坐标压缩到原来的
轴将横坐标压缩到原来的.files/image073.gif) 倍(纵坐标不变)得到
倍(纵坐标不变)得到.files/image232.gif) 的图象,故选A.
的图象,故选A.
8.在点(0,一1)处目标函数取得最大值为9,故选D.
9.先在后三位中选两个位置填两个数字“.files/image234.gif) 种填法,再排另两张卡片有
种填法,再排另两张卡片有.files/image236.gif) 种排
种排
法,再决定用数字“.files/image238.gif) 个四位数,
个四位数,
故选B.
10.依题意.files/image240.gif) ,∴
,∴.files/image242.gif) ,故选B.
,故选B.
11.因为函数.files/image097.gif) 在其定义域内为减函数,所以
在其定义域内为减函数,所以
.files/image245.gif) 恒成立,即
恒成立,即.files/image247.gif) 为减函数(切线斜率减小),故选A.
为减函数(切线斜率减小),故选A.
12..files/image249.gif) ,
,
∵.files/image251.gif) ,∴
,∴.files/image253.gif) ,当A、F、B
,当A、F、B
三点共线时取得最小值,故选C.
二、填空题(每题5分.共20分}
13.3 14..files/image255.gif) 15.28 16.①③
15.28 16.①③
简答与提示:
13.∵V正四面体 .files/image257.gif) ,∴
,∴.files/image259.gif) .
.
14.∵.files/image261.gif) ,∴
,∴.files/image263.gif) ,∴
,∴.files/image265.gif) .
.
15.∵.files/image267.gif) ,
,
∴.files/image269.gif) ,∴
,∴.files/image271.gif) .
.
16.∵.files/image273.gif) ,
,
∴.files/image275.gif) ,
,
∵.files/image277.gif) ,
,
∴.files/image279.gif) ,故①③正确.
,故①③正确.
三、解答题(满分70分)
17.本小题主要考查三角函数的基本公式、三角恒等变换、三角函数图象及性质.
解:(1)∵.files/image281.gif)
.files/image283.gif) (4分)
(4分)
∴.files/image285.gif) .
.
(2)当.files/image287.gif) ,即
,即.files/image289.gif) 时,
时,.files/image291.gif) ,
, (6分)
,
, (6分)
当.files/image293.gif) ,即
,即.files/image295.gif) ,
,.files/image297.gif) ,
,
∴函数.files/image138.gif) 的值域为[
的值域为[.files/image300.gif) ,1].
(10分)
,1].
(10分)
18.本小题主要考查概率的基本知识与分类思想,考查运用数学知识分析问题解决问题的
能力.
解.(1)中一等奖的概率为.files/image302.gif) ,
(2分)
,
(2分)
中二等奖的概率为.files/image304.gif) ,
(4分)
,
(4分)
中三等奖的概率为.files/image306.gif) ,
(6分)
,
(6分)
∴摇奖一次中奖的概率为.files/image308.gif) (7分)
(7分)
(2) 由(1)可知,摇奖一次不中奖的概率为.files/image310.gif) (9分)
(9分)
设摇奖一次庄家所获得的金额为随机变量.files/image312.gif) ,则随机变量
,则随机变量.files/image312.gif) 的分布列为:
的分布列为:
.files/image312.gif)
.files/image316.gif)
.files/image318.gif)
.files/image320.gif)
.files/image322.gif)
.files/image165.gif)
.files/image325.gif)
.files/image327.gif)
.files/image329.gif)
.files/image331.gif)
∴.files/image333.gif)
∴摇奖一次庄家获利金额的期望值为.files/image335.gif) 元 (12分)
元 (12分)
19.本小题主要考查空间线面位置关系、异面直线所成角、二面角等基本知识,考查空间想象能力、逻辑思维能力和运算能力以及空间向量的应用.
解法一:(1)证明:
.files/image337.jpg) 取
取.files/image103.gif) 中点为
中点为.files/image159.gif) ,连结
,连结.files/image220.gif) 、
、.files/image342.gif) ,
,
∵△.files/image344.gif) 是等边三角形,
是等边三角形,
∴.files/image346.gif)
又∵侧面.files/image344.gif)
.files/image348.gif) 底面
底面.files/image143.gif) ,
,
∴.files/image351.gif) 底面
底面.files/image143.gif) ,
,
∴.files/image342.gif) 为
为.files/image354.gif) 在底面
在底面.files/image143.gif) 上的射影,
上的射影,
又∵.files/image147.gif) ,
,
.files/image358.gif) ,
,
∴.files/image360.gif) ,
,
∴.files/image362.gif) ,
,
∴.files/image364.gif) ,
,
∴.files/image153.gif) .
.
(2)取.files/image354.gif) 中点
中点.files/image368.gif) ,连结
,连结.files/image370.gif) 、
、.files/image372.gif) ,
(6分)
,
(6分)
∵.files/image374.gif) .
.
∴.files/image376.gif) .
.
又∵.files/image153.gif) ,
,.files/image378.gif) ,
,
∴.files/image380.gif) 平面
平面.files/image382.gif) ,
,
∴.files/image380.gif)
.files/image372.gif) ,
,
∴.files/image386.gif) 是二面角
是二面角.files/image157.gif) 的平面角.
(9分)
的平面角.
(9分)
∵.files/image147.gif) ,
,.files/image389.gif) ,
,
∴.files/image391.gif) .
.
∴.files/image393.gif) ,
,
∴.files/image395.gif) ,
,
∴.files/image397.gif) ,
,
∴二面角.files/image157.gif) 的大小为
的大小为.files/image069.gif) (12分)
(12分)
解法二:证明:(1) 取.files/image103.gif) 中点为
中点为.files/image159.gif) ,
,.files/image400.gif) 中点为
中点为.files/image107.gif) ,连结
,连结.files/image403.gif) ,
,
∵△.files/image344.gif) 是等边三角形,
是等边三角形,
∴.files/image346.gif) ,
,
又∵侧面.files/image344.gif)
.files/image348.gif) 底面
底面.files/image143.gif) ,
,
.files/image405.jpg) ∴
∴.files/image351.gif) 底面
底面.files/image143.gif) ,
,
∴以.files/image159.gif) 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系
如图, (2分)
∵.files/image147.gif) ,△
,△.files/image344.gif) 是等边三角形,
是等边三角形,
∴.files/image408.gif) ,
,
∴.files/image410.gif) .
.
∴.files/image412.gif) .
.
∵.files/image414.gif)
∴.files/image153.gif) .
.
(2)设平面.files/image416.gif) 的法向量为
的法向量为.files/image418.gif)
∵.files/image420.gif)
∴.files/image422.gif)
令.files/image424.gif) ,则
,则.files/image426.gif) ,∴
,∴.files/image428.gif) (8分)
(8分)
设平面.files/image430.gif) 的法向量为
的法向量为.files/image432.gif) ,
,
∵.files/image434.gif) ,
,
∴.files/image436.gif) ,
,
令.files/image438.gif) ,则
,则.files/image440.gif) ,∴
,∴.files/image442.gif) (10分)
(10分)
∴.files/image444.gif) ,
,
∴.files/image446.gif) ,
,
∴二面角.files/image157.gif) 的大小为
的大小为.files/image069.gif) .
(12分)
.
(12分)
20.本小题主要考查直线、椭圆等平面解析几何的基础知识,考查轨迹的求法以及综合解题能力
解:(1)设.files/image448.gif) ,则
,则.files/image450.gif)
∵.files/image452.gif) ,∴
,∴.files/image454.gif) ,∴
,∴.files/image456.gif) ,
(3分)
,
(3分)
又.files/image458.gif) ,∴
,∴.files/image460.gif)
∴曲线.files/image169.gif) 的方程为
的方程为.files/image460.gif) (6分)
(6分)
(2)由(1)可知,.files/image107.gif) (4,0)为椭圆
(4,0)为椭圆.files/image460.gif) 的右焦点,设直线
的右焦点,设直线.files/image173.gif) 方程为
方程为
.files/image467.gif) ,由
,由.files/image469.gif) 消去
消去.files/image071.gif) 得,
得,.files/image472.gif) ,
,
∴.files/image474.gif) (9分)
(9分)
∴.files/image476.gif)
.files/image478.gif) ,
,
当.files/image480.gif) ,即
,即.files/image482.gif) 时取得最大值,
时取得最大值,
此时直线方程为.files/image484.gif) .
(12分)
.
(12分)
21.本小题主要考察等差数列定义、通项、数列求和、不等式等基础知识,考察综合分析问题的能力和推理论证能力.
解:(1)∵.files/image486.gif) ,
,
∴.files/image488.gif) (2分)
(2分)
∴.files/image490.gif) ,
,
∵.files/image188.gif) ∴
∴.files/image493.gif) .
(4分)
.
(4分)
∵.files/image495.gif) ∴
∴.files/image497.gif) ,∴
,∴.files/image499.gif) ,
,
∴.files/image501.gif) ,
,
∴数列.files/image190.gif) 是以2为首项,以1为公差的等差数列,
是以2为首项,以1为公差的等差数列,
∴.files/image504.gif) ,∴
,∴.files/image506.gif) ,
,
∴.files/image508.gif) .
(7分)
.
(7分)
(2).files/image510.gif) ,
,
∵.files/image512.gif)
.files/image514.gif)
∴.files/image516.gif) (10分)
(10分)
当.files/image518.gif) 时,
时,.files/image520.gif)
.files/image522.gif) ,
,
当.files/image524.gif) 时,
时,.files/image526.gif) ,
,
∴.files/image528.gif) .
(12分)
.
(12分)
22.本小题主要考查函数的单调性、最值、不等式等基础知识,考查运用导数研究函数性质
的方法,考查分析问题和解决问题的能力.
解:(1)∵.files/image530.gif)
∴.files/image532.gif) ,
(1分)
,
(1分)
设.files/image534.gif) .
.
∴.files/image536.gif) ,
,
∴.files/image538.gif) (1+z)在
(1+z)在.files/image540.gif) 上为减函数.
(3分)
上为减函数.
(3分)
∴.files/image542.gif) ,
,
∴.files/image544.gif) ,
,
∴函数.files/image546.gif) 在
在.files/image548.gif) 上为减函数.
(5分)
上为减函数.
(5分)
(2).files/image203.gif) 在
在.files/image548.gif) 上恒成立,
上恒成立,
.files/image552.gif) 在
在.files/image548.gif) 上恒成立,
(6分)
上恒成立,
(6分)
设.files/image554.gif) ,则
,则.files/image556.gif) ,
,
∴.files/image558.gif) ,
(7分)
,
(7分)
若.files/image560.gif) ,则
,则.files/image562.gif) 时,
时,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com