
题目列表(包括答案和解析)
 已知全集U=R,A={x|x(x+2)<0},B={x|x+1<0},则下列表示图中阴影部分的集合为( )
已知全集U=R,A={x|x(x+2)<0},B={x|x+1<0},则下列表示图中阴影部分的集合为( )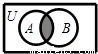
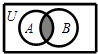 已知全集U=R,A={x|x(x+2)<0},B={x|x+1<0},则下列表示图中阴影部分的集合为
已知全集U=R,A={x|x(x+2)<0},B={x|x+1<0},则下列表示图中阴影部分的集合为一、选择题:
1. C 2. D 3. A 4 . C 5. C 6. B 7. C 8. B 9. D 10. B
二、填空题:
11. -13 12. 试题.files/image214.gif) 13. 100π 14.
13. 100π 14. 试题.files/image216.gif) 15. 0
15. 0
三、解答题:
16. (1) f(x)=(试题.files/image139.gif) +
+试题.files/image141.gif) )2+sin 2x=3cos2x+sin2x+sin2x=2cos(2x-)+2
)2+sin 2x=3cos2x+sin2x+sin2x=2cos(2x-)+2
函数f(x)的最小值是0,f(x)的最大值是试题.files/image218.gif)
(2) -1<t<试题.files/image220.gif)
17.(1)一次摸奖从试题.files/image222.gif) 个球中任取两个,有
个球中任取两个,有试题.files/image224.gif) 种方法。它们是等可能的,其中两个球的颜色不同的方法有
种方法。它们是等可能的,其中两个球的颜色不同的方法有试题.files/image226.gif) 种,一次摸奖中奖的概率
种,一次摸奖中奖的概率试题.files/image150.gif)
试题.files/image228.gif) ……6分
……6分
(2)设每次摸奖中奖的概率为试题.files/image230.gif) ,三次摸奖中(每次摸奖后放回)恰有一次中奖的概率是
,三次摸奖中(每次摸奖后放回)恰有一次中奖的概率是试题.files/image232.gif)
试题.files/image234.gif) ,
,
试题.files/image236.gif) 因而
因而试题.files/image150.gif) 在
在试题.files/image239.gif) 上为增函数,
上为增函数,
试题.files/image150.gif) 在
在试题.files/image241.gif) 上为减函数,
……9分
上为减函数,
……9分
(用重要不等式确定p值的参照给分)
∴当试题.files/image243.gif) 时
时试题.files/image150.gif) 取得最大值,即
取得最大值,即试题.files/image246.gif) ,解得
,解得试题.files/image248.gif) 或
或试题.files/image250.gif) (舍去),则当
(舍去),则当试题.files/image248.gif) 时,三次摸奖(每次摸奖后放回)恰有一次中奖的概率最大. ……12分
时,三次摸奖(每次摸奖后放回)恰有一次中奖的概率最大. ……12分
试题.files/image252.gif) 18.【方法一】证明:在线段BC1上取中点F,连结EF、DF
18.【方法一】证明:在线段BC1上取中点F,连结EF、DF
则由题意得EF∥DA1,且EF=DA1,
∴四边形EFDA1是平行四边形
∴A1E∥FD,又A1E试题.files/image254.gif) 平面BDC1,FD
平面BDC1,FD试题.files/image256.gif) 平面BDC1
平面BDC1
∴A1E∥平面BDC1 …6分
(2)由A1E⊥B
EH⊥BC1于H,连结A1H,则∠A1HE为二面角A1-BC1-B1的平面角 …8分
在Rt△BB
又A1E=2,∴tan∠A1HE==
∴二面角A1-BC1-B1为arctan …12分
试题.files/image257.gif) 【方法二】建立如图所示的空间直角坐标系,题意知B(-2,0,0),
【方法二】建立如图所示的空间直角坐标系,题意知B(-2,0,0),
D(2,40),A1(2,8,0), C1(0,8,2),B1(-2,8,0), E(-1,8,),
试题.files/image259.gif) =(-4,-4,0),
=(-4,-4,0), 试题.files/image261.gif) =(-2,4,2),
=(-2,4,2),试题.files/image263.gif) =(-3,0, ),
=(-3,0, ),
试题.files/image265.gif) =(-4,-8, 0),
=(-4,-8, 0), 试题.files/image267.gif) =(-2,0, 2),
=(-2,0, 2),试题.files/image269.gif) =(0,8,0),
=(0,8,0),
试题.files/image271.gif) =(2,8, 2).
=(2,8, 2).
(1)证明:∵试题.files/image263.gif) =2(
=2(试题.files/image259.gif) +
+试题.files/image261.gif) )∴A1E∥平面BDC1 …6分
)∴A1E∥平面BDC1 …6分
(2)设试题.files/image273.gif) =(x,y,1)为平面A1BC1的一个法向量,则
=(x,y,1)为平面A1BC1的一个法向量,则试题.files/image275.gif) ,且
,且试题.files/image277.gif) ,即
,即试题.files/image279.gif) 解得
解得试题.files/image281.gif) ∴
∴试题.files/image273.gif) =(
=(试题.files/image283.gif) ,
,试题.files/image285.gif) ,1),同理,设
,1),同理,设试题.files/image287.gif) =(x,y,1)为平面B1BC1的一个法向量,则
=(x,y,1)为平面B1BC1的一个法向量,则试题.files/image289.gif) ,且
,且试题.files/image291.gif) ,即
,即试题.files/image293.gif) 解得
解得试题.files/image295.gif) ∴
∴试题.files/image287.gif) =(-
=(-试题.files/image283.gif) ,0,1),∴cos<
,0,1),∴cos<试题.files/image273.gif) ,
,试题.files/image287.gif) >=
>=试题.files/image300.gif) =-
=-试题.files/image302.gif)
∴二面角A1-BC1-B1为arccos试题.files/image304.gif) .
…12分
.
…12分
19. (1)由题意,知a=试题.files/image306.gif) …5分
…5分
(2)设P(2cosθ, sinθ),M(4,m),N(4,n),则A(-2,0),B(2,0),
试题.files/image307.gif) 由A、P、M三点共线,得m=
由A、P、M三点共线,得m=试题.files/image309.gif) …7分
…7分
由B、P、N三点共线,得n=试题.files/image311.gif) ,
…9分
,
…9分
设Q(t,0),则由试题.files/image166.gif) 得
得
(t-4)(t-4)+(0-试题.files/image309.gif) )(0-
)(0-试题.files/image311.gif) )=0,
)=0,
整理得:(t-4)2-9=0 解得t=1或t=7
∴Q点的坐标是(7,0)或(1,0). …12分
20.20.解:(1)
(2)
21.解: (1)∵试题.files/image319.gif) ,
,
由题设可知:试题.files/image321.gif) 即
即试题.files/image323.gif)
试题.files/image325.gif) sinθ≥1 ∴sinθ=1. …4分
sinθ≥1 ∴sinθ=1. …4分
从而a= ,∴f(x)= x3+x2-2x+c,而又由f(1)= 得c=.
∴f(x)= x3+x2-2x+即为所求. …6分
(2)由试题.files/image327.gif) =(x+2)(x-1),易知f(x)在(-∞,-2)及(1,+∞)上均为增函数,在(-2,1)上为减函数.
…8分
=(x+2)(x-1),易知f(x)在(-∞,-2)及(1,+∞)上均为增函数,在(-2,1)上为减函数.
…8分
①当m>1时,f(x)在[m,m+3]上递增,故f(x)max=f(m+3), f(x)min=f(m)
由f(m+3)-f(m)= (m+3)3+(m+3)2-2(m+3)-m3-m2+
得-5≤m≤1.这与条件矛盾,故 …10分
② 当0≤m≤1时,f(x)在[m,1]上递增, 在[1,m+3]上递增
∴f(x)min=f(1), f(x)max=max{ f(m),f(m+3) },
又f(m+3)-f(m)=
∴f(x)max= f(m+3)∴|f(x1)-f(x2)|≤f(x)max-f(x)min= f(m+3)-f(1)≤f(4)-f(1)= 恒成立. …12分
故当0≤m≤1时,原不等式恒成立.综上,存在m且m∈[0,1]合题意. …13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com