练习册

  • 练习册
  • 试题
    设函数f(x)=loga(x-3a)(a>0且a≠1),当点P(x,y)是函数y=f(x)图象上的点时.点Q(x-2a,-y)是函数y=g(x)图象上的点.(1)写出函数y=g(x)的解析式,(2)若当x∈［a+2,a+3］时.恒有|f(x)-g(x)|≤1,试确定a的取值范围. 【查看更多】

     

    题目列表(包括答案和解析)

    设函数f(x)=
    log
    1-mx
    x-1
    a
    为奇函数，g（x）=f（x）+loga（x-1）（ax+1）（ a＞1，且m≠1）．
    （1）求m值；
    （2）求g（x）的定义域；
    （3）若g（x）在[-
    5
    2
    ，-
    3
    2
    ]    上恒正，求a的取值范围．

    查看答案和解析>>

    设函数f(x)=loga(1-
    ax
    )    ，其中0＜a＜1，
    （1）证明：f（x）是（a，+∞）上的减函数；
    （2）解不等式f（x）＞1．

    查看答案和解析>>

    设函数f(x)=loga
    x-2
    x+2
    ，x∈[m，n]    是单调减函数，值域为[1+loga（n-1），1+loga（m-1）]．
    （1）求实数a的取值范围；
    （2）求证：2＜m＜4＜n；
    （3）若函数g(x)=1+loga(x-1)-loga
    x-2
    x+2
    ，x∈[m，n]    的最大值为A，求证：0＜A＜1．

    查看答案和解析>>

    设函数f(x)=
    loga(x+1) ，(x＞0)
    x2+ax+b ，(x≤0).
    若f（3）=2，f（-2）=0，则b=（　　）

    查看答案和解析>>

    设函数f (x)＝loga(ax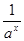＋)．(1)判断函数f (x)的奇偶性；

    (2)判断函数f (x)在(0，＋∞)的单调性并证明．

     

    查看答案和解析>>

    难点磁场

    解：(1)由6ec8aac122bd4f6e>0,且2－x≠0得F(x)的定义域为(－1，1)，设－1＜x1＜x2＜1,则

    F(x2)－F(x1)=(6ec8aac122bd4f6e)+(6ec8aac122bd4f6e)

    6ec8aac122bd4f6e,

    ∵x2－x1>0,2－x1>0,2－x2>0,∴上式第2项中对数的真数大于1.

    因此F(x2)－F(x1)>0,F(x2)>F(x1),∴F(x)在(－1，1）上是增函数.

    (2)证明：由y=f(x)=6ec8aac122bd4f6e得：2y=6ec8aac122bd4f6e,

    ∴f－1(x)=6ec8aac122bd4f6e,∵f(x)的值域为R，∴f-－1(x)的定义域为R.

    当n≥3时，f-1(n)>6ec8aac122bd4f6e.

    用数学归纳法易证2n>2n+1(n≥3),证略.

    (3)证明：∵F(0)=6ec8aac122bd4f6e,∴F－1(6ec8aac122bd4f6e)=0,∴x=6ec8aac122bd4f6e是F－1(x)=0的一个根.假设F－1(x)=0还有一个解x0(x0≠6ec8aac122bd4f6e),则F-1(x0)=0,于是F(0)=x0(x0≠6ec8aac122bd4f6e).这是不可能的，故F-1(x)=0有惟一解.

    歼灭难点训练

    一、1.解析：由题意：g(x)+h(x)=lg(10x+1)                                                                      ①

    又g(－x)+h(－x)=lg(10－x+1).即－g(x)+h(x)=lg(10－x+1)                                             ②

    由①②得：g(x)=6ec8aac122bd4f6e,h(x)=lg(10x+1)－6ec8aac122bd4f6e.

    答案：C

    2.解析：当a>1时，函数y=logax的图象只能在A和C中选，又a>1时，y=(1－a)x为减函数.

    答案：B

    二、3.解析：容易求得f- －1(x)=6ec8aac122bd4f6e,从而：

    f－1(x－1)=6ec8aac122bd4f6e

    答案：6ec8aac122bd4f6e

    4.解析：由题意，5分钟后，y1=ae－nt,y2=a－ae－nt,y1=y2.∴n=6ec8aac122bd4f6eln2.设再过t分钟桶1中的水只有6ec8aac122bd4f6e,则y1=ae－n(5+t)=6ec8aac122bd4f6e,解得t=10.

    答案：10

    三、5.解：(1)设点Q的坐标为(x′,y′),则x′=x－2a,y′=－y.即x=x′+2a,y=－y′.

    ∵点P(x,y)在函数y=loga(x－3a)的图象上，∴－y′=loga(x′+2a－3a),即y′=loga6ec8aac122bd4f6e,∴g(x)=loga6ec8aac122bd4f6e.

    (2)由题意得x－3a=(a+2)－3a=－2a+2>0;6ec8aac122bd4f6e=6ec8aac122bd4f6e>0,又a>0且a≠1,∴0＜a＜1,∵|f(x)－g(x)|=|loga(x－3a)－loga6ec8aac122bd4f6e|=|loga(x2－4ax+3a2)|?|f(x)－g(x)|≤1,∴－1≤loga(x2－4ax+3a2)≤1,∵0＜a＜1,∴a+2>2a.f(x)=x2－4ax+3a2在［a+2,a+3］上为减函数，∴μ(x)=loga(x2－4ax+3a2)在［a+2,a+3］上为减函数，从而［μ(x)］max=μ(a+2)=loga(4－4a),［μ(x)］min=μ(a+3)=loga(9－6a),于是所求问题转化为求不等式组6ec8aac122bd4f6e的解.

    由loga(9－6a)≥－1解得0＜a≤6ec8aac122bd4f6e,由loga(4－4a)≤1解得0＜a≤6ec8aac122bd4f6e,

    ∴所求a的取值范围是0＜a≤6ec8aac122bd4f6e.

    6.解：f(x1)+f(x2)=logax1+logax2=logax1x2,

    ∵x1,x2∈(0,+∞),x1x2≤(6ec8aac122bd4f6e)2(当且仅当x1=x2时取“=”号)，

    当a>1时，有logax1x2≤loga(6ec8aac122bd4f6e)2,

    ∴6ec8aac122bd4f6elogax1x2≤loga(6ec8aac122bd4f6e)，6ec8aac122bd4f6e(logax1+logax2)≤loga6ec8aac122bd4f6e,

    即6ec8aac122bd4f6e6ec8aac122bd4f6ef(x1)+f(x2)］≤f(6ec8aac122bd4f6e)(当且仅当x1=x2时取“=”号)

    当0＜a＜1时，有logax1x2≥loga(6ec8aac122bd4f6e)2,

    ∴6ec8aac122bd4f6e(logax1+logax2)≥loga6ec8aac122bd4f6e,即6ec8aac122bd4f6e［f(x1)+f(x2)］≥f(6ec8aac122bd4f6e)(当且仅当x1=x2时取“=”号）.

    7.解：由已知等式得：loga2x+loga2y=(1+2logax)+(1+2logay),即(logax－1)2+(logay－1)2=4,令u=logax,v=logay,k=logaxy,则(u－1)2+(v－1)2=4(uv≥0),k=u+v.在直角坐标系uOv内，圆弧(u－1)2+(v－1)2=4(uv≥0)与平行直线系v=－u+k有公共点，分两类讨论.

    (1)当u≥0,v≥0时，即a>1时，结合判别式法与代点法得1+6ec8aac122bd4f6e≤k≤2(1+6ec8aac122bd4f6e);

    (2)当u≤0,v≤0,即0＜a＜1时，同理得到2(1－6ec8aac122bd4f6e)≤k≤1－6ec8aac122bd4f6e.x综上，当a>1时，logaxy的最大值为2+26ec8aac122bd4f6e，最小值为1+6ec8aac122bd4f6e；当0＜a＜1时，logaxy的最大值为1－6ec8aac122bd4f6e，最小值为2－26ec8aac122bd4f6e.

    8.解：∵2(6ec8aac122bd4f6ex)2+9(6ec8aac122bd4f6ex)+9≤0

    ∴(26ec8aac122bd4f6ex+3)( 6ec8aac122bd4f6ex+3)≤0.

    ∴－3≤6ec8aac122bd4f6ex≤－6ec8aac122bd4f6e.

    即6ec8aac122bd4f6e (6ec8aac122bd4f6e)－3≤6ec8aac122bd4f6ex≤6ec8aac122bd4f6e(6ec8aac122bd4f6e)6ec8aac122bd4f6e?

    ∴(6ec8aac122bd4f6e)6ec8aac122bd4f6e≤x≤(6ec8aac122bd4f6e)－3,∴26ec8aac122bd4f6e≤x≤8

    即M={x|x∈［26ec8aac122bd4f6e,8］}

    又f(x)=(log2x－1)(log2x－3)=log22x－4log2x+3=(log2x－2)2－1.

    ∵26ec8aac122bd4f6e≤x≤8,∴6ec8aac122bd4f6e≤log2x≤3

    ∴当log2x=2,即x=4时ymin=－1;当log2x=3,即x=8时，ymax=0.

     

     

     


    同步练习册答案