
题目列表(包括答案和解析)
(1)求证:AD⊥BC;
(2)求二面角B-AC—D的大小;
(3)(理)在线段AC上是否存在一点E,使ED与平面BCD成30°角?若存在,确定点E的位置;若不存在,说明理由.

第21题图
 在直角梯形ABCD中,AD∥BC,
在直角梯形ABCD中,AD∥BC,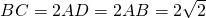 ,∠ABC=90°,如图1.把△ABD沿BD翻折,使得平面ABD⊥平面BCD,如图2.
,∠ABC=90°,如图1.把△ABD沿BD翻折,使得平面ABD⊥平面BCD,如图2.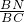 的值;若不存在,说明理由.
的值;若不存在,说明理由. 设D是△ABC的BC边上一点,把△ACD沿AD折起,使C点所处的新位置C′在平面ABD上的射影H恰好在AB上.
设D是△ABC的BC边上一点,把△ACD沿AD折起,使C点所处的新位置C′在平面ABD上的射影H恰好在AB上.设D是△ABC的BC边上一点,把△ACD沿AD折起,使C点所处的新位置C′在平面ABD上的射影H恰好在AB上.
(1)求证:直线C′D与平面ABD和平面AHC′所成的两个角之和不可能超过90°;
(2)若∠BAC=90°,二面角C′—AD—H为60°,求∠BAD的正切值.
???

难点磁场
(1)证明:作NA⊥α于A,MB⊥β于B,连接AP、PB、BN、AM,再作AC⊥l于C,BD⊥l于D,连接NC、MD.
∵NA⊥α,MB⊥β,∴∠MPB、∠NPA分别是MP与β所成角及NP与α所成角,∠MNB,∠NMA分别是MN与β,α所成角,∴∠MPB=∠NPA.
在Rt△MPB与Rt△NPA中,PM=PN,∠MPB=∠NPA,∴△MPB≌△NPA,∴MB=NA.
在Rt△MNB与Rt△NMA中,MB=NA,MN是公共边,∴△MNB≌△NMA,∴∠MNB=∠NMA,即(1)结论成立.
(2)解:设∠MNB=θ,MN= a,则PB=PN=a,MB=NA=
a,则PB=PN=a,MB=NA= asinθ,NB=
asinθ,NB= acosθ?,∵MB⊥β,BD⊥l,∴MD⊥l,∴∠MDB是二面角α―l―β的平面角,
acosθ?,∵MB⊥β,BD⊥l,∴MD⊥l,∴∠MDB是二面角α―l―β的平面角,
∴∠MDB=60°,同理∠NCA=60°,
∵MB⊥β,MP⊥PN,∴BP⊥PN
∵∠BPN=90°,∠DPB=∠CNP,∴△BPD∽△PNC,∴
整理得,16sin4θ-16sin2θ+3=0
解得sin2θ= ,sinθ=
,sinθ= ,当sinθ=
,当sinθ= 时,CN=
时,CN= asinθ=
asinθ=  a>PN不合理,舍去.
a>PN不合理,舍去.
歼灭难点训练
一、1.解析:(特殊位置法)将P点取为A1,作OE⊥AD于E,连结A1E,则A1E为OA1的射影,又AM⊥A1E,∴AM⊥OA1,即AM与OP成90°角.
答案:D
2.解析:作AO⊥CB的延长线,连OD,则OD即为AD在平面BCD上的射影,
答案:B
二、3.解析:在OC上取一点C,使OC=1,过C分别作CA⊥OC交OA于A,CB⊥OC交OB于B,则AC=1,,OA= ,BC=
,BC= ,OB=2,Rt△AOB中,AB2=6,△ABC中,由余弦定理,得cosACB=-
,OB=2,Rt△AOB中,AB2=6,△ABC中,由余弦定理,得cosACB=- .
.
4.解析:设一个侧面面积为S1,底面面积为S,则这个侧面在底面上射影的面积为 ,由题设得
,由题设得 ,设侧面与底面所成二面角为θ,则cosθ=
,设侧面与底面所成二面角为θ,则cosθ= ,∴θ=60°.
,∴θ=60°.
答案:60°
三、5.(1)解:因为PA⊥平面AC,AB⊥BC,∴PB⊥BC,即∠PBC=90°,由勾股定理得PB= .
.
(2)解:如图,过点C作CE∥BD交AD的延长线于E,连结PE,则PC与BD所成的角为∠PCE或它的补角.
(3)证明:设PB、PC中点分别为G、F,连结FG、AG、DF,则GF∥BC∥AD,且GF= BC=1=AD,从而四边形ADFG为平行四边形,
BC=1=AD,从而四边形ADFG为平行四边形,
又AD⊥平面PAB,∴AD⊥AG,即ADFG为矩形,DF⊥FG.
从而DF⊥平面PBC,故平面PDC⊥平面PBC,即二面角B―PC―D为直二面角.?
6.解:(1)如图,在平面ABC内,过A作AH⊥BC,垂足为H,则AH⊥平面DBC,
∴∠ADH即为直线AD与平面BCD所成的角.由题设知△AHB≌△AHD,则DH⊥BH,AH=DH,
∴∠ADH=45°
(2)∵BC⊥DH,且DH为AD在平面BCD上的射影,
∴BC⊥AD,故AD与BC所成的角为90°.
(3)过H作HR⊥BD,垂足为R,连结AR,则由三垂线定理知,AR⊥BD,故∠ARH为二面角A―BD―C的平面角的补角.设BC=a,则由题设知,AH=DH= ,在△HDB中,HR=
,在△HDB中,HR= a,∴tanARH=
a,∴tanARH= =2
=2
故二面角A―BD―C大小为π-arctan2.
7.(1)证明:取BC中点E,连结AE,∵AB=AC,∴AE⊥BC
∵平面ABC⊥平面BCD,∴AE⊥平面BCD,
∵BC⊥CD,由三垂线定理知AB⊥CD.
∴平面ABD⊥平面ACD.
(2)解:在面BCD内,过D作DF∥BC,过E作EF⊥DF,交DF于F,由三垂线定理知AF⊥DF,∠ADF为AD与BC所成的角.
(3)解:∵AE⊥面BCD,过E作EG⊥BD于G,连结AG,由三垂线定理知AG⊥BD,
∴∠AGE为二面角A―BD―C的平面角
又AE= m,∴tanAGE=
m,∴tanAGE= =2,∴∠AGE=arctan2.
=2,∴∠AGE=arctan2.
即二面角A―BD―C的大小为arctan2.
8.(1)证明:连结DH,∵C′H⊥平面ABD,∴∠C′DH为C′D与平面ABD所成的角且平面C′HA⊥平面ABD,过D作DE⊥AB,垂足为E,则DE⊥平面C′HA.
故∠DC′E为C′D与平面C′HA所成的角
∴∠DC′E≤∠DC′H,
∴∠DC′E+∠C′DE≤∠DC′H+∠C′DE=90°
(2)解:作HG⊥AD,垂足为G,连结C′G,
则C′G⊥AD,故∠C′GH是二面角C′―AD―H的平面角
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com