
题目列表(包括答案和解析)
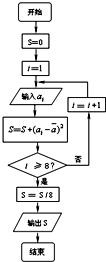 对一个作直线运动的质点的运动过程观测了8次,第i次观测得到的数据为ai,具体如下表所示:
对一个作直线运动的质点的运动过程观测了8次,第i次观测得到的数据为ai,具体如下表所示:| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ai | 40 | 41 | 43 | 43 | 44 | 46 | 47 | 48 |
. |
| a |
| A、6 | B、7 | C、8 | D、9 |
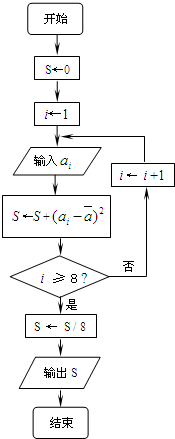 对一个作直线运动的质点的运动过程观测了8次,第i次观测得到的数据为ai,具体如下表所示:
对一个作直线运动的质点的运动过程观测了8次,第i次观测得到的数据为ai,具体如下表所示:| 观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 观测数据ai | 40 | 41 | 43 | 43 | 44 | 46 | 47 | 48 |
. |
| a |
对一个作直线运动的质点的运动过程观测了8次,得到如下表所示的数据:
| 观测次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 观测数据 | 40 | 41 | 43 | 43 | 44 | 46 | 47 | 48 |
在上述数据的统计分析中,一部分计算见如下图所示的程序框图(其中![]() 是这8个数据的平均数),则输出的
是这8个数据的平均数),则输出的![]() 的值是______。
的值是______。
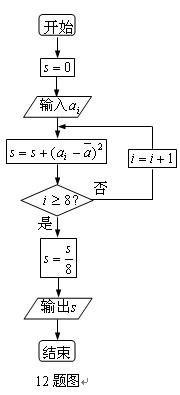
对一个作直线运动的质点的运动过程观测了8次,
得到如下表所示的数据:
| 观测次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 观测数据 | 40 | 41 | 43 | 43 | 44 | 46 | 47 | 48 |
在上述统计数据的分析中,一部分计算见如图所示的程序
框图(其中![]() 是这8个数据的平均数),则输出的
是这8个数据的平均数),则输出的![]() 的值
的值
是__________.
|
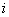 次观测得到的数据为
次观测得到的数据为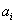 ,具体如下表所示:
,具体如下表所示:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
40 |
41 |
43 |
43 |
44 |
46 |
47 |
48 |
在对上述统计数据的分析中,一部分计算见如图所示的
算法流程图(其中 是这8个数据的平均数),则输出的
是这8个数据的平均数),则输出的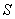
的值是 ( )
A.6 B.7
C. 8 D.9
2009.3
一、选择题
(1)B (2)A (3)B (4)C (5)B (6)D
(7)D (8)C (9)C (10)B (11)A (12)C
二、填空题
|