
题目列表(包括答案和解析)
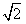 a,
a,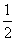 AB;②AB=
AB;②AB=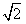 a;③CM⊥AB;④BC⊥AC。请你从中再选择两个条件以确定cosθ的值,并求解.
a;③CM⊥AB;④BC⊥AC。请你从中再选择两个条件以确定cosθ的值,并求解. 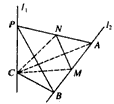
如图,已知圆锥体 的侧面积为
的侧面积为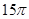 ,底面半径
,底面半径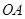 和
和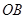 互相垂直,且
互相垂直,且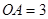 ,
, 是母线
是母线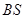 的中点.
的中点.

(1)求圆锥体的体积;
(2)异面直线 与
与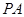 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
【解析】本试题主要考查了圆锥的体积和异面直线的所成的角的大小的求解。
第一问中,由题意, 得
得 ,故
,故
从而体积 .2中取OB中点H,联结PH,AH.
.2中取OB中点H,联结PH,AH.
由P是SB的中点知PH//SO,则 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.在
AH.在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
解:(1)由题意, 得
得 ,
,
故 从而体积
从而体积 .
.
(2)如图2,取OB中点H,联结PH,AH.
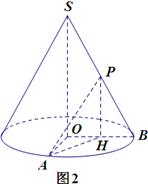
由P是SB的中点知PH//SO,则 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.
AH.
在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识,考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分
【解析】(Ⅰ)解:由所给数据可知,一等品零件共有6个.设“从10个零件中,随机抽取一个为一等品”为事件A,则P(A)=![]() =
=![]() .
.
(Ⅱ)(i)解:一等品零件的编号为![]() .从这6个一等品零件中随机抽取2个,所有可能的结果有:
.从这6个一等品零件中随机抽取2个,所有可能的结果有:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 共有15种.
共有15种.
(ii)解:“从一等品零件中,随机抽取的2个零件直径相等”(记为事件B)的所有可能结果有:![]() ,
,![]() ,共有6种.
,共有6种.
所以P(B)=![]() .
.
(本小题满分12分)
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=![]() ,∠BAD=∠CDA=45°.
,∠BAD=∠CDA=45°.
 (Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅱ)证明CD⊥平面ABF;
(Ⅲ)求二面角B-EF-A的正切值。
零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识,考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分
【解析】(Ⅰ)解:由所给数据可知,一等品零件共有6个.设“从10个零件中,随机抽取一个为一等品”为事件A,则P(A)=![]() =
=![]() .
.
(Ⅱ)(i)解:一等品零件的编号为![]() .从这6个一等品零件中随机抽取2个,所有可能的结果有:
.从这6个一等品零件中随机抽取2个,所有可能的结果有:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 共有15种.
共有15种.
(ii)解:“从一等品零件中,随机抽取的2个零件直径相等”(记为事件B)的所有可能结果有:![]() ,
,![]() ,共有6种.
,共有6种.
所以P(B)=![]() .
.
(本小题满分12分)
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=![]() ,∠BAD=∠CDA=45°.
,∠BAD=∠CDA=45°.
 (Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅱ)证明CD⊥平面ABF;
(Ⅲ)求二面角B-EF-A的正切值。
(本小题满分12分)
有编号为![]() ,
,![]() ,…
,…![]() 的10个零件,测量其直径(单位:cm),得到下面数据:
的10个零件,测量其直径(单位:cm),得到下面数据:

其中直径在区间[1.48,1.52]内的零件为一等品。
(Ⅰ)从上述10个零件中,随机抽取一个,求这个零件为一等品的概率;
(Ⅱ)从一等品零件中,随机抽取2个.
(ⅰ)用零件的编号列出所有可能的抽取结果;
(ⅱ)求这2个零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识,考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分
【解析】(Ⅰ)解:由所给数据可知,一等品零件共有6个.设“从10个零件中,随机抽取一个为一等品”为事件A,则P(A)=![]() =
=![]() .
.
(Ⅱ)(i)解:一等品零件的编号为![]() .从这6个一等品零件中随机抽取2个,所有可能的结果有:
.从这6个一等品零件中随机抽取2个,所有可能的结果有:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 共有15种.
共有15种.
(ii)解:“从一等品零件中,随机抽取的2个零件直径相等”(记为事件B)的所有可能结果有:![]() ,
,![]() ,共有6种.
,共有6种.
所以P(B)=![]() .
.
(本小题满分12分)
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=![]() ,∠BAD=∠CDA=45°.
,∠BAD=∠CDA=45°.
 (Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅱ)证明CD⊥平面ABF;
一、 填空题:
1、 2、
2、 3、128 4、
3、128 4、 5、64 6、
5、64 6、
7、 8、
8、 9、-4 10、15 11、
9、-4 10、15 11、
12、(1)(2)(5)
二、选择题:
13、D 14、 C 15、 B 16、 C
17、解:以A为原点,以AB、AD、AP所在直线分别 轴,
轴,
建立空间直角坐标系。 -----2分
则 C(2,1,0) N(1,0,1)  =(-1,-1,1)---4分
=(-1,-1,1)---4分
D(0,2,0) M(1, ,1)
,1)  =(1,-
=(1,- ,1)---6分
,1)---6分
设 与
与 的夹角为
的夹角为 ,
,
 ----8分
----8分
 ---10分
---10分
 异面直线
异面直线 与
与 所成的角为
所成的角为 -----12分
-----12分
18、解:延长 ,作
,作 交
交 于D,------4分
于D,------4分
设 ,则
,则
 ------8分
------8分
解得 .------10分
.------10分
故船继续朝原方向前进有触礁的危险.-----12
19、解: (1)因为f(x+y)=f(x)+f(y),
令x=y=0,代入①式,-----2分
得f(0+0)=f(0)+f(0),即 f(0)=0 --------4分
(2)令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,
则有0=f(x)+f(-x).------6分
即f(-x)=-f(x)对任意x∈R成立,
所以f(x)是奇函数.......8分
(3) f(3)=log 3>0,即f(3)>f(0),
3>0,即f(3)>f(0),
又f(x)在R上是单调函数,所以f(x)在R上是增函数,----10分
又由(1)f(x)是奇函数.
f(k?3 )<-f(3
)<-f(3 -9
-9 -2)=f(-3
-2)=f(-3 +9
+9 +2),
+2),
k?3 <-3
<-3 +9
+9 +2,
+2,
得 ------12分
------12分

 ------------14分
------------14分
20、解:(1) 为等差数列,∵
为等差数列,∵ ,又
,又 ,
,
∴  ,
, 是方程
是方程 的两个根
的两个根
又公差 ,∴
,∴ ,∴
,∴ ,
, -------- 2分
-------- 2分
∴  ∴
∴ ∴
∴ -----------4分
-----------4分
(2)由(1)知, -----------5分
-----------5分
∴
∴ ,
, ,
, ------------7分
------------7分
∵ 是等差数列,∴
是等差数列,∴ ,∴
,∴ ----------8分
----------8分
∴ (
( 舍去)
------------9分
舍去)
------------9分
(3)由(2)得 -------------11分
-------------11分
 ,
, 时取等号 ------- 13分
时取等号 ------- 13分
 ,
, 时取等号15分
时取等号15分
(1)、(2)式中等号不可能同时取到,所以 -----------16分
-----------16分
21、解:(1)椭圆 与
与 相似. -----2分
相似. -----2分
因为 的特征三角形是腰长为4,底边长为
的特征三角形是腰长为4,底边长为 的等腰三角形,
的等腰三角形,
而椭圆 的特征三角形是腰长为2,
的特征三角形是腰长为2,
底边长为 的等腰三角形,
的等腰三角形,
因此两个等腰三角形相似,且相似比为 .
---
6分
.
---
6分
(2)椭圆 的方程为:
的方程为: .
--------8分
.
--------8分
假定存在,则设 、
、 所在直线为
所在直线为 ,
, 中点为
中点为 .
.
则
 .
-------10分
.
-------10分
所以 .
.
中点在直线 上,所以有
上,所以有 . ----12分
. ----12分
 .
.
 . -------14分
. -------14分
(3)椭圆 的方程为:
的方程为: .
.
两个相似椭圆之间的性质有: 写出一个给2分
① 两个相似椭圆的面积之比为相似比的平方;
② 分别以两个相似椭圆的顶点为顶点的四边形也相似,相似比即为椭圆的相似比;
③ 两个相似椭圆被同一条直线所截得的线段中点重合;
过原点的直线截相似椭圆所得线段长度之比恰为椭圆的相似比. ----20分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com