题目列表(包括答案和解析)
（本小题满分12分）
中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次：“酒后驾车”和“醉酒驾车”，其检测标准是驾驶人员血液中的酒精含量Q（简称血酒含量，单位是毫克/100毫升），当20≤Q≤80时，为酒后驾车；当Q＞80时，为醉酒驾车.济南市公安局交通管理部门于2011年2月的某天晚上8点至11点在市区设点进行一次拦查行动，共依法查出了60名饮酒后违法驾驶机动车者，如图为这60名驾驶员抽血检测后所得结果画出的频率分布直方图（其中Q≥140的人数计入120≤Q＜140人数之内）.
|
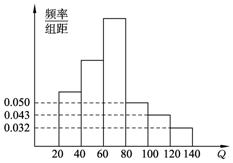
（Ⅰ） 求此次拦查中醉酒驾车的人数；
（Ⅱ） 从违法驾车的60人中按酒后驾车和醉酒驾车利用分层抽样抽取8人做样本进行研究，再从抽取的8人中任取3人，求3人中含有醉酒驾车人数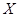
的分布列和期望.
|
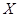的分布列和期望.（本小题满分12分）
某学校举办消防知识竞赛，总共 7 个题中，分值为 10 分的有 
共4 个，分值为 20 分的有 
共3个，每位选手都要分别从 4 个 10 分题和 3 个 20 分题中各随机抽取 1 题参赛．已知甲选手 4 个 10 分题中只有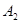 
不会，3个
20 分题中只会
．
（Ⅰ）求甲选手恰好得30分的概率；
（Ⅱ）求甲选手得分超过10分的概率．
（本题满分12分）
现有编号分别为1，2，3的三个不同的政治基本题和一道政治附加题：另有编号分别为
4，5的两个不同的历史基本题和一道历史附加题。甲同学从这五个基本题中一次随即抽取两道题，每题做对做错及每题被抽到的概率是相等的。
（1）用符号（
）表示事件“抽到的两题的编号分别为
、
，且
”共有多少个基本事件？请列举出来：
（2）求甲同学所抽取的两道基本题的编号之和小于8但不小于4的概率。
（3）甲同学在抽完两道基本题之后又抽取一道附加题，做对基本题每题加5分，做对政治附加题加10分，做对历史附加题加15分，求甲同学得分不低于20分的概率。
（本题满分12分）
现有编号分别为1，2，3的三个不同的政治基本题和一道政治附加题：另有编号分别为
4，5的两个不同的历史基本题和一道历史附加题。甲同学从这五个基本题中一次随即抽取两道题，每题做对做错及每题被抽到的概率是相等的。
（1）用符号（
）表示事件“抽到的两题的编号分别为
、
，且
”共有多少个基本事件？请列举出来：
（2）求甲同学所抽取的两道基本题的编号之和小于8但不小于4的概率。
（3）甲同学在抽完两道基本题之后又抽取一道附加题，做对基本题每题加5分，做对政治附加题加10分，做对历史附加题加15分，求甲同学得分不低于20分的概率。
一、 填空题：
1、
2、
3、128 4、
5、64 6、
7、
8、
9、-4 10、15 11、
12、（1）（2）（5）
二、选择题：
13、D 14、 C 15、 B 16、 C
17、解：以A为原点，以AB、AD、AP所在直线分别
轴，
建立空间直角坐标系。 -----2分
则 C（2，1，0） N（1，0，1） 
=（-1，-1，1）---4分
D（0，2，0） M（1，
，1） 
=（1，-
，1）---6分
设与的夹角为
，
----8分
---10分
异面直线
与
所成的角为 -----12分
18、解：延长
，作
交于D，------4分
设
，则
------8分
解得
．------10分
故船继续朝原方向前进有触礁的危险．-----12
19、解： (1)因为f(x+y)=f(x)+f(y)，
令x=y=0，代入①式，-----2分
得f(0+0)=f(0)+f(0)，即 f(0)=0 --------4分
（２）令y=-x，代入①式，得 f(x-x)=f(x)+f(-x)，又f(0)=0，
则有0=f(x)+f(-x)．------6分
即f(-x)=-f(x)对任意x∈R成立，
所以f(x)是奇函数．．．．．．．8分
(3) f(3)=log
3＞0，即f(3)＞f(0)，
又f(x)在R上是单调函数，所以f(x)在R上是增函数，----10分
又由(1)f(x)是奇函数．
f(k?3
)＜-f(3-9-2)=f(-3+9+2)，
k?3＜-3+9+2，
得
------12分
------------１4分
20、解：（1）
为等差数列，∵
，又
，
∴ 
，
是方程
的两个根
又公差
，∴
，∴
，
-------- 2分
∴ 
∴
∴
-----------4分
（2）由(1)知，
-----------5分
∴
∴
，
，
------------7分
∵
是等差数列，∴
，∴
----------8分
∴
（
舍去）
------------9分
（3）由(2)得
-------------11分
，
时取等号 ------- 13分
，
时取等号15分
(1)、(2)式中等号不可能同时取到，所以
-----------16分
21、解：（1）椭圆
与
相似. -----2分
因为的特征三角形是腰长为4，底边长为
的等腰三角形，
而椭圆的特征三角形是腰长为2，
底边长为
的等腰三角形，
因此两个等腰三角形相似，且相似比为
.
---
6分
（2）椭圆
的方程为：
.
--------8分
假定存在，则设
、
所在直线为
，
中点为
.
则
.
-------10分
所以
.
中点在直线
上，所以有
. ----12分
.
. -------14分
（3）椭圆的方程为：.
两个相似椭圆之间的性质有： 写出一个给2分
① 两个相似椭圆的面积之比为相似比的平方；
② 分别以两个相似椭圆的顶点为顶点的四边形也相似，相似比即为椭圆的相似比；
③ 两个相似椭圆被同一条直线所截得的线段中点重合；
过原点的直线截相似椭圆所得线段长度之比恰为椭圆的相似比. ----20分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com