练习册

  • 练习册
  • 试题
    从而判别式-------14分 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分14分）广东某民营企业主要从事美国的某品牌运动鞋的加工生产，按国际惯例以美元为结算货币，依据以往加工生产的数据统计分析，若加工产品订单的金额为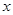万美元，可获得加工费近似为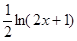万美元，受美联储货币政策的影响，美元贬值,由于生产加工签约和成品交付要经历一段时间，收益将因美元贬值而损失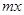万美元，其中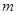为该时段美元的贬值指数，，从而实际所得的加工费为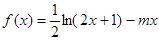（万美元）.

    （Ⅰ）若某时期美元贬值指数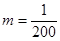，为确保企业实际所得加工费随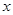的增加而增加，该企业加工产品订单的金额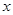应在什么范围内？

    （Ⅱ）若该企业加工产品订单的金额为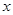万美元时共需要的生产成本为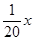万美元，已知该企业加工生产能力为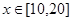（其中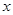为产品订单的金额），试问美元的贬值指数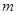在何范围时，该企业加工生产将不会出现亏损.

     

    查看答案和解析>>

    本题有（1）、（2）、（3）三个小题，每题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分
    （1）已知
    10
    12
    B=
    -43
    4-1
    ，求矩阵B．
    （2）已知极点与原点重合，极轴与x轴正半轴重合，若曲线C1的极坐标方程为：ρcos(θ-
    π
    4
    )=
    		2
    ，曲线C2的参数方程为：
    x=2cosθ
    y=
    		3
    sinθ
    （θ为参数），试求曲线C1、C2的交点的直角坐标．
    （3）已知x2+2y2+3z2=
    18
    17
    ，求3x+2y+z的最小值．

    查看答案和解析>>

    本题有（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
    （1）选修4-2：矩阵与变换
    已知矩阵M=
    01
    10
    ，N=
    0-1
    10

    （Ⅰ）求矩阵NN；
    （Ⅱ）若点P（0，1）在矩阵M对应的线性变换下得到点P′，求P′的坐标．
    （2）选修4-4：坐标系与参数方程
    在直角坐标系xOy中，直线l的参数方程是
    x=t
    y=2t+1
    （t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的极坐标方程是ρ=2cosθ（Ⅰ）在直角坐标系xOy中，求圆C的直角坐标方程
    （Ⅱ）求圆心C到直线l的距离．
    （3）选修4-5：不等式选讲
    已知函数f（x）=|x-1|
    （Ⅰ）解不等式f（x）＞2；
    （Ⅱ）求函数y=f（-x）+f（x+5）的最小值．

    查看答案和解析>>

    本题有（1）、（2）、（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题记分．
    （Ⅰ）选修4-2：矩阵与变换，
    已知矩阵A=
    01
    a0
    ，矩阵B=
    02
    b0
    ，直线l1    ：x-y+4=0经矩阵A所对应的变换得直线l2，直线l2又经矩阵B所对应的变换得到直线l3：x+y+4=0，求直线l2的方程．
    （Ⅱ）选修4-4：坐标系与参数方程，
    求直线
    x=-2+2t
    y=-2t
    被曲线
    x=1+4cosθ
    y=-1+4sinθ
    截得的弦长．
    （Ⅲ）选修4-5：不等式选讲，解不等式|x+1|+|2x-4|＞6．

    查看答案和解析>>

    本题有（Ⅰ）、（Ⅱ）、（Ⅲ）三个选答题，每题7分，请考生任选两题作答，满分14分．如果多做，则按所做的前两题记分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
    （Ⅰ）直线l1：x=-4先经过矩阵A=
    4m
    n-4
    作用，再经过矩阵B=
    11
    0-1
    作用，变为直线l2：2x-y=4，求矩阵A．
    （Ⅱ）已知直线l的参数方程：
    x=t
    y=1+2t
    （t为参数）和圆C的极坐标方程：p=2
    		2
    sin（θ+
    π
    4
    ）．判断直线l和圆C的位置关系．
    （Ⅲ）解不等式：|x|+2|x-1|≤4．

    查看答案和解析>>


    同步练习册答案