
题目列表(包括答案和解析)
某城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客的需求.为此,某城市公交公司在某站台随机调查了
80名乘客,他们的候车时间如下所示(单位:min):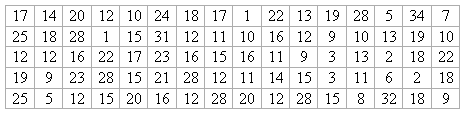
(1)
将数据进行适当的分组,并画出相应的频率分布直方图和频率折线图;(2)
这80名乘客候车时间的平均数是多少?标准差呢?(3)
你能为公交公司提出什么建议?(本小题满分12分)
数列![]() 的前
的前![]() 项和记为
项和记为![]() ,
,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)等差数列![]() 的各项为正,其前
的各项为正,其前![]() 项和为
项和为![]() 且
且![]() ,又
,又![]() 成
成
等比数列,求![]() 的通项公式;
的通项公式;
已知数列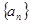 中,
中, ,点
,点 在直线
在直线 上,其中
上,其中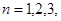 …。
…。
(1)令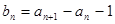 ,证明数列
,证明数列 是等比数列;
是等比数列;
(2)设 分别为数列
分别为数列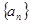 、
、 的前
的前 项和,证明数列
项和,证明数列 是等差数列。
是等差数列。
【解析】本试题主要考查了等差数列和等比数列的通项公式以及数列的求和的综合运用问题。既考查了概念,又考查了同学们的计算能力。
已知数列 中,
中, ,
, ,数列
,数列 中,
中, ,且点
,且点 在直线
在直线 上。
上。
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)若 ,求数列
,求数列 的前
的前 项和
项和 ;
;
【解析】第一问中利用数列的递推关系式
 ,因此得到数列
,因此得到数列 的通项公式;
的通项公式;
第二问中, 在
在 即为:
即为:
即数列 是以
是以 的等差数列
的等差数列
得到其前n项和。
第三问中, 又
又 

 ,利用错位相减法得到。
,利用错位相减法得到。
解:(1)
 即数列
即数列 是以
是以 为首项,2为公比的等比数列
为首项,2为公比的等比数列

 ……4分
……4分
(2) 在
在 即为:
即为:
即数列 是以
是以 的等差数列
的等差数列

 ……8分
……8分
(3) 又
又 


 ①
①  ②
②
①- ②得到


(本小题满分12分)
数列 的前
的前 项和记为
项和记为 ,
,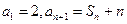 .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)等差数列 的各项为正,其前
的各项为正,其前 项和为
项和为 且
且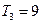 ,又
,又 成
成
等比数列.
(1)求 的通项公式;
的通项公式;
(2)求证:当 时,
时, .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com