
题目列表(包括答案和解析)
 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
 的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 和
和 判断C2与C1是否相似,如果相似则求出C2与C1的相似比,若不相似请说明理由;
判断C2与C1是否相似,如果相似则求出C2与C1的相似比,若不相似请说明理由;
如图,已知椭圆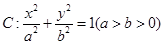 的焦点和上顶点分别为
的焦点和上顶点分别为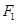 、
、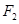 、
、 ,我们称
,我们称 为椭圆
为椭圆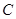 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
(1)已知椭圆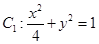 和
和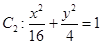 ,判断
,判断 与
与 是否相似,如果相似则求出
是否相似,如果相似则求出 与
与 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;
(2)若与椭圆 相似且半短轴长为
相似且半短轴长为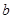 的椭圆为
的椭圆为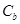 ,且直线
,且直线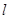 与椭圆为
与椭圆为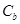 相交于两点
相交于两点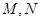 (异于端点),试问:当
(异于端点),试问:当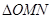 面积最大时,
面积最大时,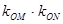 是否与
是否与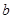 有关?并证明你的结论.
有关?并证明你的结论.
(3)根据与椭圆 相似且半短轴长为
相似且半短轴长为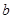 的椭圆
的椭圆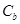 的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
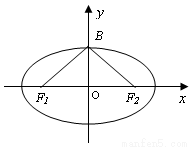
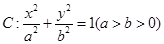 的焦点和上顶点分别为
的焦点和上顶点分别为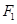 、
、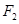 、
、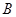 ,我们称
,我们称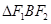 为椭圆
为椭圆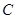 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 和
和 ,判断
,判断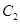 与
与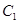 是否相似,如果相似则求出
是否相似,如果相似则求出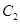 与
与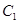 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;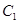 相似且半短轴长为
相似且半短轴长为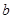 的椭圆为
的椭圆为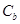 ,且直线
,且直线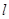 与椭圆为
与椭圆为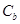 相交于两点
相交于两点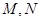 (异于端点),试问:当
(异于端点),试问:当 面积最大时,
面积最大时,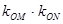 是否与
是否与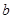 有关?并证明你的结论.
有关?并证明你的结论.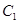 相似且半短轴长为
相似且半短轴长为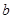 的椭圆
的椭圆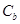 的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com