
题目列表(包括答案和解析)
直线x-y=2被圆(x-a)2+y2=4所截得的弦长为2![]() ,则实数a的值为
,则实数a的值为
-1或![]()
1或3
-2或6
0或4
直线![]() x-y+m=0与圆x2+y2-2x-2=0相切,则实数m等于
x-y+m=0与圆x2+y2-2x-2=0相切,则实数m等于
-3![]() 或
或![]()
-![]() 或
或![]()
![]() 或-
或-![]()
-3![]() 或
或![]()
直线![]() x-y+m=0与圆x2+y2-2x-2=0相切,则实数m等于
x-y+m=0与圆x2+y2-2x-2=0相切,则实数m等于
A.![]() 或
或![]()
B.![]() 或
或![]()
C.![]() 或
或![]()
D.![]() 或
或![]()
若直线![]() x-y-1=0到直线x-ay=0的角为
x-y-1=0到直线x-ay=0的角为![]() ,则实数a等于
,则实数a等于
A.0 B.![]()
C.0或![]() D.-
D.-![]()
若直线x-y=2被圆(x-a)2+y2=4所截得的弦长为2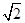 ,则实数a的值为
,则实数a的值为
A.-1或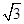 B.1或3 C.-2或6 D.0或4
B.1或3 C.-2或6 D.0或4
难点磁场
解:由l过原点,知k= (x0≠0),点(x0,y0)在曲线C上,y0=x03-3x02+2x0,
(x0≠0),点(x0,y0)在曲线C上,y0=x03-3x02+2x0,
y′=3x2-6x+2,k=3x02-6x0+2
歼灭难点训练
一、1.解析:y′=esinx[cosxcos(sinx)-cosxsin(sinx)],y′(0)=e0(1-0)=1
答案:B
2.解析:设切点为(x0,y0),则切线的斜率为k= ,另一方面,y′=(
,另一方面,y′=( )′=
)′= ,故
,故
y′(x0)=k,即 或x02+18x0+45=0得x0(1)=-3,y0(2)=-15,对应有y0(1)=3,y0(2)=
或x02+18x0+45=0得x0(1)=-3,y0(2)=-15,对应有y0(1)=3,y0(2)= ,因此得两个切点A(-3,3)或B(-15,
,因此得两个切点A(-3,3)或B(-15, ),从而得y′(A)=
),从而得y′(A)= =-1及y′(B)=
=-1及y′(B)=  ,由于切线过原点,故得切线:lA:y=-x或lB:y=-
,由于切线过原点,故得切线:lA:y=-x或lB:y=- .
.
答案:A
答案:-1
4.解析:设g(x)=(x+1)(x+2)……(x+n),则f(x)=xg(x),于是f′(x)=g(x)+xg′(x),f′(0)=g(0)+0?g′(0)=g(0)=1?2?…n=n!
答案:n!
三、5.解:设l与C1相切于点P(x1,x12),与C2相切于Q(x2,-(x2-2)2)
对于C1:y′=2x,则与C1相切于点P的切线方程为
y-x12=2x1(x-x1),即y=2x1x-x12 ①
对于C2:y′=-2(x-2),与C2相切于点Q的切线方程为y+(x2-2)2=-2(x2-2)(x-x2),即y=-2(x2-2)x+x22-4 ②
∵两切线重合,∴2x1=-2(x2-2)且-x12=x22-4,解得x1=0,x2=2或x1=2,x2=0
∴直线l方程为y=0或y=4x-4
6.解:(1)注意到y>0,两端取对数,得
lny=ln(x2-2x+3)+lne2x=ln(x2-2x+3)+2x
(2)两端取对数,得
两边解x求导,得
7.解:设经时间t秒梯子上端下滑s米,则s=5- ,当下端移开1.4 m时,t0=
,当下端移开1.4 m时,t0= ,又s′=-
,又s′=- (25-9t2)
(25-9t2) ?(-9?2t)=9t
?(-9?2t)=9t ,所以s′(t0)=9×
,所以s′(t0)=9× =0.875(m/s)
=0.875(m/s)
8.解:(1)当x=1时,Sn=12+22+32+…+n2= n(n+1)(2n+1),当x≠1时,1+2x+3x2+…+nxn-1?=
n(n+1)(2n+1),当x≠1时,1+2x+3x2+…+nxn-1?= ,两边同乘以x,得
,两边同乘以x,得
Sn=12+22x2+32x2+…+n2xn-1?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com