
题目列表(包括答案和解析)
如果直线![]() ,
,![]() 的斜率分别是二次方程:
的斜率分别是二次方程:![]() 的两根,那么
的两根,那么![]() 和
和![]() 所成的角是_____
所成的角是_____
A、![]() B、
B、 ![]() C、
C、![]() D、
D、![]()
如果两条直线的斜率分别是一元二次方程x2-4x+1=0的两个根,那么这两条直线所成的角是________.
平面直角坐标系内的向量都可以用一有序实数对唯一表示,这使我们想到可以用向量作为解析几何的研究工具.如图,设直线
l的倾斜角为α(α≠90°).在l上任取两个不同的点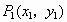 ,
, ,不妨设向量
,不妨设向量 的方向是向上的,那么向量
的方向是向上的,那么向量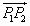 的坐标是(
的坐标是( ).过原点作向量
).过原点作向量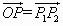 ,则点P的坐标是(
,则点P的坐标是( ),而且直线OP的倾斜角也是α.根据正切函数的定义得
),而且直线OP的倾斜角也是α.根据正切函数的定义得
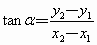 ,
,
这就是《数学
2》中已经得到的斜率公式.上述推导过程比《数学2》中的推导简捷.你能用向量作为工具讨论一下直线的有关问题吗?例如:(1)
过点 ,平行于向量
,平行于向量 的直线方程;
的直线方程;
(2)
向量(A,B)与直线 的关系;
的关系;
(3)
设直线 和
和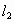 的方程分别是
的方程分别是
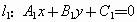
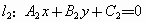
那么,
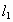 ∥
∥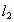 ,
,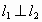 的条件各是什么?如果它们相交,如何得到它们的夹角公式?
的条件各是什么?如果它们相交,如何得到它们的夹角公式?
(4)
点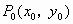 到直线
到直线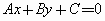 的距离公式如何推导?
的距离公式如何推导?
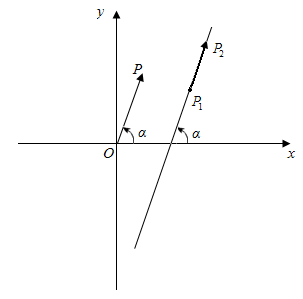
1―10.CAACB CCCDB,11.(1,1),12.(-2,3),13.5 ,14.D=E,15.m>-1/2
,14.D=E,15.m>-1/2
16.因为x2-y2=0表示过原点的两条互相垂直的直线:y=x,y=-x,(x-a)2+y2=1表示圆心为C(a,0),半径为1的动圆,本题讨论方程组有实数解的问题即讨论圆与直线有公共点的问题。(1)- ≤a≤
≤a≤ ;(2)当-
;(2)当- <a<-1或-1<a<1或1<a<
<a<-1或-1<a<1或1<a< 时有四组实数解,当a=±1时,有三组实数解,当a=±
时有四组实数解,当a=±1时,有三组实数解,当a=± 时,有两组实数解,当a<-
时,有两组实数解,当a<- 或a>
或a> 时无实数解。
时无实数解。
17.以直线AB为x轴,线段AB的垂直平分线为y轴建立直角坐标系。设A(-5,0),则B(5,0),在平面内任取一点P(x,y),设从A运货物到P的运费为
 即P点在圆C
即P点在圆C
 的内部.换言之,圆C内部的居民应在A地购买,同理可推得圆C外部的应在B地购物,圆C上的居民可随意选择A、B两地之一购物。
的内部.换言之,圆C内部的居民应在A地购买,同理可推得圆C外部的应在B地购物,圆C上的居民可随意选择A、B两地之一购物。
 18.尝试使用对称法,如图作A点关于y轴
18.尝试使用对称法,如图作A点关于y轴
的对称点A1,再作A点关于y=x的对称点A2,
在y轴和y=x上公别取点B、 C,则|BA|=|BA1|,
|AC|=|A
|AB|+|BC|+|CA|=|A1B|+|BC|+|CA2|,
从而将问题转化为在y轴,y=x上各取一点,使
折线A1BCA2的长度最小。B(0,-17/5)和C(-17/8,-17/8)
19.(1)配方得圆心,将心坐标消去m可得直线a:x-3y-3=0
(2)设与直线a平行的直线c:x-3y+b=0(b≠-3),则圆心到直线a的距离为
 ,∵圆的半径r=5,∴当d<r时,直线与圆相交,当d=r时,直线与圆相切,当d>r时直线与圆相离。(3)对于任一条平行于a且与圆相交的直线的直线c,由于圆心到直线c的距离都与m无关,所以弦长与m无关。
,∵圆的半径r=5,∴当d<r时,直线与圆相交,当d=r时,直线与圆相切,当d>r时直线与圆相离。(3)对于任一条平行于a且与圆相交的直线的直线c,由于圆心到直线c的距离都与m无关,所以弦长与m无关。
 20.△ABC为直角三角形,如国图建立直角坐标系,
20.△ABC为直角三角形,如国图建立直角坐标系,
则A(0,0)、B(4,0)、C(0,3),设内切圆半径
为r,则r=1/2(|OC|+|OB|-|BC|)=1,故内切圆方程为
(x-1)2+(y-1)2=1,可设P点坐标(1+Cosα,1+Sinα)
则以PA、PB、PC为直径的三个圆面积之和S= (10-Cosα)
(10-Cosα)
当Cosα=-1时,Smax=5.5π,
当Cosα=1时, Smin=4.5π.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com