
题目列表(包括答案和解析)
平抛运动及其规律
1.平抛运动:将物体用一定的初速度沿________方向抛出,不考虑空气阻力,物体只在________作用下的运动.
2.平抛运动的处理方法:可分解成水平方向的________运动和竖直方向的________运动两个方向的分运动.
3.平抛运动的规律:
水平方向:匀速直线运动vx=v0,x=x0t,ax=0
竖直方向:自由落体运动vy=gt,![]() ,ay=g
,ay=g
合运动(实际运动):![]() ,a=g
,a=g
4.平抛运动的性质:做平抛运动的物体仅受重力的作用,故平抛运动是________曲线运动.
5.平抛运动的常用推论:①做平抛运动的物体任意时刻的瞬时速度的反向延长线与初速度方向延长线的交点到抛出点的距离都等于水平位移的一半.
②平抛运动中以抛点O为坐标原点的坐标系中任一点A(x,y)的速度方向与竖直方向的夹角为α,如图,则tanα=x/2y
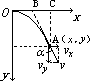
第三部分 运动学
第一讲 基本知识介绍
一. 基本概念
1. 质点
2. 参照物
3. 参照系——固连于参照物上的坐标系(解题时要记住所选的是参照系,而不仅是一个点)
4.绝对运动,相对运动,牵连运动:v绝=v相+v牵
二.运动的描述
1.位置:r=r(t)
2.位移:Δr=r(t+Δt)-r(t)
3.速度:v=limΔt→0Δr/Δt.在大学教材中表述为:v=dr/dt, 表示r对t 求导数
5.以上是运动学中的基本物理量,也就是位移、位移的一阶导数、位移的二阶导数。可是

三阶导数为什么不是呢?因为牛顿第二定律是F=ma,即直接和加速度相联系。(a对t的导数叫“急动度”。)
6.由于以上三个量均为矢量,所以在运算中用分量表示一般比较好
三.等加速运动
v(t)=v0+at r(t)=r0+v0t+1/2 at2

一道经典的物理问题:二次世界大战中物理学家曾经研究,当大炮的位置固定,以同一速度v0沿各种角度发射,问:当飞机在哪一区域飞行之外时,不会有危险?(注:结论是这一区域为一抛物线,此抛物线是所有炮弹抛物线的包络线。此抛物线为在大炮上方h=v2/2g处,以v0平抛物体的轨迹。)
练习题:
一盏灯挂在离地板高l2,天花板下面l1处。灯泡爆裂,所有碎片以同样大小的速度v 朝各个方向飞去。求碎片落到地板上的半径(认为碎片和天花板的碰撞是完全弹性的,即切向速度不变,法向速度反向;碎片和地板的碰撞是完全非弹性的,即碰后静止。)
四.刚体的平动和定轴转动
1. 我们讲过的圆周运动是平动而不是转动
2. 角位移φ=φ(t), 角速度ω=dφ/dt , 角加速度ε=dω/dt
3. 有限的角位移是标量,而极小的角位移是矢量
4. 同一刚体上两点的相对速度和相对加速度
 两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上
两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上
投影:[VA]AB=[VB]AB,aA=aB+aAB,aAB=,anAB+,aτAB, ,aτAB垂直于AB,,anAB=VAB2/AB
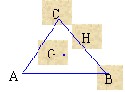
例:A,B,C三质点速度分别VA ,VB ,VC
求G的速度。
五.课后习题:
一只木筏离开河岸,初速度为V,方向垂直于岸边,航行路线如图。经过时间T木筏划到路线上标有符号处。河水速度恒定U用作图法找到在2T,3T,4T时刻木筏在航线上的确切位置。
五、处理问题的一般方法
(1)用微元法求解相关速度问题
例1:如图所示,物体A置于水平面上,A前固定一滑轮B,高台上有一定滑轮D,一根轻绳一端固定在C点,再绕过B、D,BC段水平,当以恒定水平速度v拉绳上的自由端时,A沿水平面前进,求当跨过B的两段绳子的夹角为α时,A的运动速度。
(vA=![]() )
)
(2)抛体运动问题的一般处理方法
(1)将斜上抛运动分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动
(2)将沿斜面和垂直于斜面方向作为x、y轴,分别分解初速度和加速度后用运动学公式解题
(3)将斜抛运动分解为沿初速度方向的斜向上的匀速直线运动和自由落体运动两个分运动,用矢量合成法则求解
例2:在掷铅球时,铅球出手时距地面的高度为h,若出手时的速度为V0,求以何角度掷球时,水平射程最远?最远射程为多少?
(α=![]() 、 x=
、 x=![]() )
)
第二讲 运动的合成与分解、相对运动
(一)知识点点拨

参考系的转换:动参考系,静参考系
相对运动:动点相对于动参考系的运动
绝对运动:动点相对于静参考系统(通常指固定于地面的参考系)的运动
牵连运动:动参考系相对于静参考系的运动
(5)位移合成定理:SA对地=SA对B+SB对地
速度合成定理:V绝对=V相对+V牵连
加速度合成定理:a绝对=a相对+a牵连
(二)典型例题
(1)火车在雨中以30m/s的速度向南行驶,雨滴被风吹向南方,在地球上静止的观察者测得雨滴的径迹与竖直方向成21。角,而坐在火车里乘客看到雨滴的径迹恰好竖直方向。求解雨滴相对于地的运动。
提示:矢量关系入图
答案:83.7m/s
(2)某人手拿一只停表,上了一次固定楼梯,又以不同方式上了两趟自动扶梯,为什么他可以根据测得的数据来计算自动扶梯的台阶数?
提示:V人对梯=n1/t1
V梯对地=n/t2
V人对地=n/t3
V人对地= V人对梯+ V梯对地
答案:n=t2t3n1/(t2-t3)t1

(3)某人驾船从河岸A处出发横渡,如果使船头保持跟河岸垂直的方向航行,则经10min后到达正对岸下游120m的C处,如果他使船逆向上游,保持跟河岸成а角的方向航行,则经过12.5min恰好到达正对岸的B处,求河的宽度。
提示:120=V水*600
D=V船*600
答案:200m
(4)一船在河的正中航行,河宽l=100m,流速u=5m/s,并在距船s=150m的下游形成瀑布,为了使小船靠岸时,不至于被冲进瀑布中,船对水的最小速度为多少?
提示:如图船航行
答案:1.58m/s
(三)同步练习
1.一辆汽车的正面玻璃一次安装成与水平方向倾斜角为β1=30°,另一次安装成倾角为β2=15°。问汽车两次速度之比![]() 为多少时,司机都是看见冰雹都是以竖直方向从车的正面玻璃上弹开?(冰雹相对地面是竖直下落的)
为多少时,司机都是看见冰雹都是以竖直方向从车的正面玻璃上弹开?(冰雹相对地面是竖直下落的)
2、模型飞机以相对空气v=39km/h的速度绕一个边长2km的等边三角形飞行,设风速u = 21km/h ,方向与三角形的一边平行并与飞机起飞方向相同,试求:飞机绕三角形一周需多少时间?
3.图为从两列蒸汽机车上冒出的两股长幅气雾拖尾的照片(俯视)。两列车沿直轨道分别以速度v1=50km/h和v2=70km/h行驶,行驶方向如箭头所示,求风速。
4、细杆AB长L ,两端分别约束在x 、 y轴上运动,(1)试求杆上与A点相距aL(0< a <1)的P点运动轨迹;(2)如果vA为已知,试求P点的x 、 y向分速度vPx和vPy对杆方位角θ的函数。

(四)同步练习提示与答案
1、提示:利用速度合成定理,作速度的矢量三角形。答案为:3。
2、提示:三角形各边的方向为飞机合速度的方向(而非机头的指向);
第二段和第三段![]() 大小相同。
大小相同。
参见右图,显然:
v2 = ![]() + u2 - 2v合ucos120°
+ u2 - 2v合ucos120°
可解出 v合 = 24km/h 。
答案:0.2hour(或12min.)。
3、提示:方法与练习一类似。答案为:3
4、提示:(1)写成参数方程![]() 后消参数θ。
后消参数θ。
(2)解法有讲究:以A端为参照, 则杆上各点只绕A转动。但鉴于杆子的实际运动情形如右图,应有v牵 = vAcosθ,v转 = vA![]() ,可知B端相对A的转动线速度为:v转 + vAsinθ=
,可知B端相对A的转动线速度为:v转 + vAsinθ= ![]() 。
。
P点的线速度必为 ![]() = v相
= v相
所以 vPx = v相cosθ+ vAx ,vPy = vAy - v相sinθ
答案:(1)![]() +
+ ![]() = 1 ,为椭圆;(2)vPx = avActgθ ,vPy =(1 - a)vA
= 1 ,为椭圆;(2)vPx = avActgθ ,vPy =(1 - a)vA
曲线运动万有引力.files/image232.jpg)
曲线运动万有引力.files/image234.jpg) 一、选择题
一、选择题
1、根据图象分析:若沿x轴作匀速运动,通过图1分析可知,y方向先减速后加速;若沿y轴方向作匀速运动,通过图2分析可知,x方向先加速后减速。
答案:B
2、乙船能到达A点,则vcos600=u,
曲线运动万有引力.files/image235.jpg) 过河时间t满足:t = H/( vsin600), 甲、乙两船沿垂直于河岸方向的分速度相同,故过河时间相同。在t时间内甲船沿河岸方向的位移为s= (vcos600 + u )t=
过河时间t满足:t = H/( vsin600), 甲、乙两船沿垂直于河岸方向的分速度相同,故过河时间相同。在t时间内甲船沿河岸方向的位移为s= (vcos600 + u )t=曲线运动万有引力.files/image191.gif) 。
。
答案:D
3、根据万有引力定律:曲线运动万有引力.files/image237.gif) ,得:T=
,得:T=曲线运动万有引力.files/image197.gif)
答案:A
4、质点在A、B、C、D四点离开轨道,分别做下抛、平抛、上抛、平抛运动。很明显,在A点离开轨道比在C、D两点离开轨道在空间时间短。通过计算在A点下抛落地时间为tA=(6曲线运动万有引力.files/image240.gif) -4)s,在B点平抛落地时间tB=4
-4)s,在B点平抛落地时间tB=4曲线运动万有引力.files/image242.gif) s,显然,在A点离开轨道后在空中时间最短。根据机械能守恒,在D刚抛出时机械能最大,所以落地时速度最大。
s,显然,在A点离开轨道后在空中时间最短。根据机械能守恒,在D刚抛出时机械能最大,所以落地时速度最大。
答案:AD
曲线运动万有引力.files/image207.jpg) 5、在轨道上向其运行方向弹射一个物体,由于质量远小于空间站的质量,空间站仍沿原方向运动。根据动量守恒,弹出后一瞬间,空间站沿原运行方向的速度变小,提供的向心力(万有引力)大于需要的向心力,轨道半径减小,高度降低,在较低的轨道上运行速率变大,周期变小。
5、在轨道上向其运行方向弹射一个物体,由于质量远小于空间站的质量,空间站仍沿原方向运动。根据动量守恒,弹出后一瞬间,空间站沿原运行方向的速度变小,提供的向心力(万有引力)大于需要的向心力,轨道半径减小,高度降低,在较低的轨道上运行速率变大,周期变小。
答案:C
6、当悬线在竖直状态与钉相碰时根据能量守恒可知,小球速度不变;但圆周运动的半径减小,需要的向心力变大,向心加速度变大,绳子上的拉力变大。
答案:BD
7、根据万有引力定律:曲线运动万有引力.files/image237.gif) 可得:M=
可得:M=曲线运动万有引力.files/image244.gif) ,可求出恒星质量与太阳质量之比,根据
,可求出恒星质量与太阳质量之比,根据曲线运动万有引力.files/image246.gif) 可得:v=
可得:v=曲线运动万有引力.files/image248.gif) ,可求出行星运行速度与地球公转速度之比。
,可求出行星运行速度与地球公转速度之比。
答案:AD
8、卫星仍围绕地球运行,所以发射速度小
答案:CD
9、同步卫星随地球自转的方向是从东向西,把同步卫星从赤道上空3.6万千米、东经103°处,调整到104°处,相对于地球沿前进方向移动位置,需要增大相对速度,所以应先下降高度增大速度到某一位置再上升到原来的高度。
答案:A
10、开始转动时向心力由静摩擦力提供,但根据F=mrω2可知,B需要的向心力是A的两倍。所以随着转速增大,B的摩擦力首先达到最大静摩擦力。继续增大转速,绳子的张力增大,B的向心力由最大静摩擦力提供,A的向心力由静摩擦力和绳子的张力的合力提供,随着转速的增大,B需要的向心力的增量(绳子张力的增量)比A需要的向心力的增量大,因而A指向圆心的摩擦力逐渐减小直到为0然后反向增大到最大静摩擦力。所以,B受到的静摩擦力先增大,后保持不变;A受到的静摩擦力是先减小后增大;A受到的合外力就是向心力一直在增大。
答案:BD
二、填空题
11、圆盘转动时,角速度的表达式为ω= 曲线运动万有引力.files/image250.gif) , T为电磁打点计的时器打点的时间间隔,r为圆盘的半径,x2、x1是纸带上选定的两点分别对应米尺上的刻度值,n为选定的两点间的打点数(含两点)。地纸带上选取两点(间隔尽可能大些)代入上式可求得ω=
6.8rad/s。
, T为电磁打点计的时器打点的时间间隔,r为圆盘的半径,x2、x1是纸带上选定的两点分别对应米尺上的刻度值,n为选定的两点间的打点数(含两点)。地纸带上选取两点(间隔尽可能大些)代入上式可求得ω=
6.8rad/s。
12、 (1)斜槽末端切线方向保持水平;从同一高度。
(2)设时间间隔为t, x
= v0t, y2-y1=gt2
,解得: v0=曲线运动万有引力.files/image252.gif) .将x=
.将x=
三、计算题
13.解:⑴在行星表面,质量为m的物体的重力近似等于其受到的万有引力,则
曲线运动万有引力.files/image083.gif)
g=曲线运动万有引力.files/image177.gif)
得:曲线运动万有引力.files/image256.gif)
⑵行星表面的环绕速度即为第一宇宙速度,做匀速圆周运动的向心力是万有引力提供的,则
曲线运动万有引力.files/image258.gif)
v1=曲线运动万有引力.files/image248.gif)
曲线运动万有引力.files/image260.gif) 得:
得:曲线运动万有引力.files/image262.gif)
14.解析:用r表示飞船圆轨道半径,有r =R +H=6.71×l
由万有引力定律和牛顿定律,得 曲线运动万有引力.files/image264.gif) , 式中M表示地球质量,m表示飞船质量,T表示飞船绕地球运行的周期,G表示万有引力常量.
, 式中M表示地球质量,m表示飞船质量,T表示飞船绕地球运行的周期,G表示万有引力常量.
利用曲线运动万有引力.files/image167.gif) 及上式, 得
及上式, 得 曲线运动万有引力.files/image266.gif) ,代入数值解得T=5.28×103s,
,代入数值解得T=5.28×103s,
出舱活动时间t=25min23s=1523s,
航天员绕行地球角度 曲线运动万有引力.files/image268.gif) =1040
=1040
15.解:(1)这位同学对过程的分析错误,物块先沿着圆柱面加速下滑,然后离开圆柱面做斜下抛运动,离开圆柱面时的速率不等于曲线运动万有引力.files/image270.gif) 。
。
(2)a、设物块离开圆柱面时的速率为曲线运动万有引力.files/image272.gif) ,
,
曲线运动万有引力.files/image273.gif)
曲线运动万有引力.files/image275.gif)
曲线运动万有引力.files/image277.gif)
解得:曲线运动万有引力.files/image279.gif)
(2)b、由:曲线运动万有引力.files/image222.gif) 得:
得:
落地时的速率为曲线运动万有引力.files/image195.gif)
曲线运动万有引力.files/image224.gif)
16.解:对子弹和木块应用动量守恒定律:
曲线运动万有引力.files/image281.gif)
所以
曲线运动万有引力.files/image283.gif)
对子弹、木块由水平轨道到最高点应用机械能守恒定律,
取水平面为零势能面:有
曲线运动万有引力.files/image285.gif)
所以 曲线运动万有引力.files/image287.gif)
由平抛运动规律有:曲线运动万有引力.files/image289.gif)
曲线运动万有引力.files/image291.gif)
解得: 曲线运动万有引力.files/image293.gif)
所以,当R =
最大值Smax =
曲线运动万有引力.files/image294.gif)
17.解:(1)
曲线运动万有引力.files/image296.gif)
(2)设人在B1位置刚好看见卫星出现在A1位置,最后
在B2位置看到卫星从A2位置消失,
OA1=2OB1
有曲线运动万有引力.files/image298.gif) ∠A1OB1=∠A2OB2=π/3
∠A1OB1=∠A2OB2=π/3
从B1到B2时间为t
则有 曲线运动万有引力.files/image300.gif)
18.解: (1)设
A、B的圆轨道半径分别为曲线运动万有引力.files/image302.gif) 、
、曲线运动万有引力.files/image304.gif) ,由题意知,A、B做匀速圆周运动的角速 度相同,设其为
,由题意知,A、B做匀速圆周运动的角速 度相同,设其为曲线运动万有引力.files/image306.gif) 。由牛顿运动定律,有
。由牛顿运动定律,有
曲线运动万有引力.files/image308.gif)
曲线运动万有引力.files/image310.gif)
曲线运动万有引力.files/image312.gif)
设
A、B之间的距离为曲线运动万有引力.files/image314.gif) ,又
,又曲线运动万有引力.files/image316.gif) ,由上述各式得
,由上述各式得
曲线运动万有引力.files/image318.gif) , ①
, ①
由万有引力定律,有
曲线运动万有引力.files/image320.gif)
将①代入得
曲线运动万有引力.files/image322.gif)
令
曲线运动万有引力.files/image324.gif)
比较可得
曲线运动万有引力.files/image326.gif) ②
②
(2)由牛顿第二定律,有
曲线运动万有引力.files/image328.gif) ③
③
又可见星 A的轨道半径
曲线运动万有引力.files/image330.gif) ④
④
由②③④式解得
曲线运动万有引力.files/image332.gif) ⑤
⑤
(3)将曲线运动万有引力.files/image334.gif) 代入⑤式,得
代入⑤式,得
曲线运动万有引力.files/image336.gif)
代入数据得
曲线运动万有引力.files/image338.gif) ⑥
⑥
曲线运动万有引力.files/image340.gif) ,将其代入⑥式得
,将其代入⑥式得
曲线运动万有引力.files/image342.gif) ⑦
⑦
可见,曲线运动万有引力.files/image344.gif) 的值随 n的增大而增大,试令
的值随 n的增大而增大,试令曲线运动万有引力.files/image346.gif) ,得
,得
曲线运动万有引力.files/image348.gif) ⑧
⑧
若使⑦式成立,则 n 必大于 2,即暗星
B 的质量曲线运动万有引力.files/image350.gif) 必大于
必大于曲线运动万有引力.files/image352.gif) ,由此得出结
,由此得出结
论:暗星曲线运动万有引力.files/image354.gif) 有可能是黑洞。
有可能是黑洞。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com