题目列表(包括答案和解析)
| I（?10-1A） | 3.0 | 6.0 | 9.0 | 12.0 | 15.0 | 18.0 |
| UM（?10-1V） | 1.1 | 1.9 | 3.4 | 4.5 | 6.2 | 6.8 |
如图（1），将一金属薄片垂直置于磁场B中，在薄片的两个侧面a、b间通以电流I时，另外两侧c、f间产生电势差，这一现象称为霍尔效应。且满足UM＝kIB/d，式中d为薄片的厚度，k为霍尔系数。
某同学通过实验来测定该金属的霍尔系数。已知该薄片的厚度d＝0.40mm，该同学保持磁感应强度B＝0.10T不变，改变电流I的大小，测量相应的UM，记录数据如下表所示。
| I（´10－1A） | 3.0 | 6.0 | 9.0 | 12.0 | 15.0 | 18.0 |
| UM（´10－1V） | 1.1 | 1.9 | 3.4 | 4.5 | 6.2 | 6.8 |
（1）根据表中数据在给定坐标系中画出图线；
（2）利用图线求出该材料的霍尔系数k=________´10－3V·m·A－1·T－1（保留2位有效数字）；
（3）利用霍尔效应制作的霍尔元件以及传感器，广泛应用于测量和自动控制等领域。图（2）是霍尔测速仪的示意图，将非磁性圆盘固定在转轴上，圆盘的周边等距离地嵌装着m个永磁体，相邻永磁体的极性相反。霍尔元件置于被测圆盘的边缘附近。当圆盘匀速转动时，霍尔元件输出的电压脉冲信号图像如图（3）所示。若在时间t内，霍尔元件输出的脉冲数目为P，则圆盘转速N的表达式：_____________________。
 |
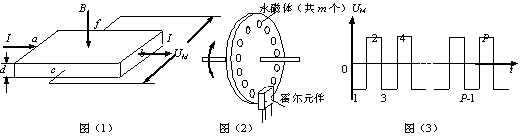
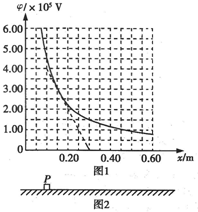粗糙绝缘的水平面附近存在一个平行于水平面的电场，其中某一区域的电场线与x轴平行，且沿x轴方向的电势φ与坐标值x的关系如下表格所示．| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| x/m | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 |
| φ/105v | 9.00 | 4.50 | 3.00 | 2.25 | 1.80 | 1.50 | 1.29 | 1.13 | 1.00 |
粗糙绝缘的水平面附近存在一个平行于水平面的电场，其中某一区域的电场线与x轴平行，且沿x轴方向的电势j与坐标值x的关系如下表格所示：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| x/m | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 |
| φ/105v | 9.00 | 4.50 | 3.00 | 2.25 | 1.80 | 1.50 | 1.29 | 1.13 | 1.00 |
根据上述表格中的数据可作出如右的j—x图像。现有一质量为0.10kg，电荷量为1.0´10-7C带正电荷的滑块（可视作质点），其与水平面的动摩擦因数为0.20。问：
（1）由数据表格和图像给出的信息，写出沿x轴的电势j与x的函数关系表达式。
（2）若将滑块无初速地放在x=0.10m处，则滑块最终停止在何处？
（3）在上述第（2）问的整个运动过程中，它的加速度如何变化？当它位于x=0.15m时它的加速度多大？（电场中某点场强为φ-t图线上某点对应的斜率）
（4）若滑块从x=0.60m处以初速度v0沿-x方向运动，要使滑块恰能回到出发点，其初速度v0应为多大？
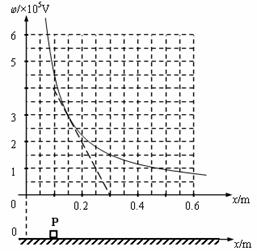
粗糙绝缘的水平面附近存在一个平行于水平面的电场，其中某一区域的电场线与x轴平行，且沿x轴方向的电势j与坐标值x的关系如下表格所示：
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| x/m | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 |
| φ/105v | 9.00 | 4.50 | 3.00 | 2.25 | 1.80 | 1.50 | 1.29 | 1.13 | 1.00 |
根据上述表格中的数据可作出如右的j—x图像。现有一质量为0.10kg，电荷量为1.0´10-7C带正电荷的滑块（可视作质点），其与水平面的动摩擦因数为0.20。问：
（1）由数据表格和图像给出的信息，写出沿x轴的电势j与x的函数关系表达式。
（2）若将滑块无初速地放在x=0.10m处，则滑块最终停止在何处？
（3）在上述第（2）问的整个运动过程中，它的加速度如何变化？当它位于x=0.15m时它的加速度多大？（电场中某点场强为j—x图线上某点对应的斜率）
（4）若滑块从x=0.60m处以初速度v0沿-x方向运动，要使滑块恰能回到出发点，其初速度v0应为多大？
第一部分 选择题（每题4分，共40分，漏选给2分，错选、不选给0分）
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
CD
C
BC
ABC
BD
AC
BD
AC
CD
AC
CD
第二部分 非选择题（共110分）
13．（1）(4分)直径读数为
（每空2分，第一空最后一位估计允许偏差±
（2）(10分)
（a）实验电路图（2分，有错给0分）
（b） 110 W， 1.10 V。
（c）电动势E＝ 1.30 V，内电阻r＝__20__W.
（每空2分，有效数字不做要求）
14．（1）（2分）还需要的实验器材是：
刻度尺、天平（配砝码） ．（每项1分）
（2）（每空2分）
还缺哪些实验步骤： 平衡摩擦力（适当垫起长木板的左端，直至轻推滑块，滑块能在水平长木板上匀速滑行为止）
应控制的实验条件： 实验中保持
．
要验证的数学表达式：
（3）（每空2分）
W＝
； ΔEK＝
．
本题第（1）、（2）问可能会出现许多不同的解答，可参考以下方案给分：
解一：（1）天平（1分） 刻度尺（1分）
（2）所缺的步骤：在沙桶中装适量的细沙，直到轻推滑块，滑块能在水平长木板上匀速运动为止（2分），用天平测出此时沙和小桶的总质量m′（2分）．
本实验最终要验证的数学表达式
（2分）
解二：（1）天平（1分） 刻度尺（1分）
（2）所缺的步骤：在沙桶中装适量的细沙直到轻推滑块，滑块能在水平长木板上匀速运动为止（2分），用天平测出此时沙和小桶的总质量m′（1分）．实验中保持．（1分）
本实验最终要验证的数学表达式
（2分）
解三：（1）天平（1分） 刻度尺（1分） 小木块（1分）
（2）所缺的步骤：先将空的小沙桶从滑轮上取下，用天平测定小沙桶的质量
（2分），再将空的小沙桶挂回，用小木块将长木板的左端稍稍垫起，直至轻推滑块，滑块能在水平长木板上匀速滑行为止（1分）．
本实验最终要验证的数学表达式（2分）
解四：（1）天平（1分） 刻度尺（1分） 小木块（1分）
（2）所缺的步骤：先将小沙桶和滑块的连线断开，用小木块将长木板的左端稍稍垫起（1分），直至轻推滑块，滑块能在水平长木板上匀速滑行为止（1分）．实验中保持．（1分）
本实验最终要验证的数学表达式
（2分）
解五：（1）天平（1分） 刻度尺（1分） 小木块（1分）
（2）所缺的步骤：先将空的小沙桶从滑轮上取下，用天平测定小沙桶的质量（1分），再将空的小沙桶挂回，用小木块将长木板的左端稍稍垫起，直至轻推滑块，滑块能在水平长木板上匀速滑行为止（1分）．实验中保持．（1分）
本实验最终要验证的数学表达式
（2分）
15．（10分）解：着陆器从高度为h处平抛到第二次着陆，由机械能守恒有：
2分
得出月球表面的重力加速度为：
………①
3分
当卫星的轨道半径为月球半径R时，发射速度最小，设最小速度为
，由万有引力（约等于重力）提供向心力有：
………② 2分
由①②式可得出：
………③ 3分
16．（12分）
解：（1）由左手定则和题意知，小球带负电 ………2分
设小球第一次到达最低点时的速度为v，则由动能定理（或由机械能守恒定律）可得：
………2分
在最低点由向心力公式得：
………2分
解得：q=2.5×10
（2）根据机械能守恒定律，小球第二次到达最低点时，速度大小仍为v………2分
由向心力公式得：
………2分
解得：F=5.5×10-2N………1分
17．(14分)
解：（1）金属杆做加速度不断减小的加速运动………2分
（2）由图象知：
时，
；
此时由于平衡
………2分
得：
………2分
（3）由图象知：
，
此时由牛顿第二定律：
………2分
即：
；………3分
解得：
………3分
18．（15分）
解：（1）因油滴在第Ⅱ、Ⅲ象限中做匀速直线运动，所以油滴受的合力为零，若油滴带负电，则其合力一定不为零；若油滴带正电，则其合力可以为零，所以油滴带正电．………3分
(2) 由平衡条件知：
………3分
………2分
（3）油滴从进入
区域到
点的过程由动能定理：
………3分
；………2分
………2分
19．(16分)
解：（1）对
球，从静止到碰
的过程由动
能定理：
；………1分
即：
得：
…1分
、碰撞由动量守恒，令水平向左为正：有：
………1分
得：
（向左）………1分
加上竖直向上的电场
后，整体
仍做圆周运动到最高点的过程由动能定理：
………1分
得： 
………1分
在最高点，由牛顿第二定律：
………1分
得：
………1分
（2）整体能完成圆周运动的条件是：在点：
………1分
即：
………1分
得：
………1分
、碰撞由动量守恒，令水平向左为正：有：
得：
………1分 由
得：
………1分
、碰撞由动量守恒，令水平向右为正：有：
得：
………1分 由
得：
………1分
所以，
满足的条件是：或………1分
20.（17分）
解：解:(1)质子在磁场中受洛仑兹力做匀速圆周运动，根据
牛顿第二定律有：
………2分
得半径为：
………2分
(2)由于质子的初速度方向与x轴正方向的夹角为300，
且半径恰好等于OA，因此质子将在磁场中做半个圆周
运动到达y轴上的C点，如图所示.
根据圆周运动的规律，质子做圆周运动的周期为:
………2分
质子从出发运动到第一次到达y轴的时间为:
………1分
质子进入电场时的速度方向与电场的方向相同，在电场中先做匀减速运动，速度减为零后反向做匀加速直线运动，设质子在电场中运动的时间为t2，根据牛顿第二定律有:
………2分，得
………1分
因此质子从开始运动到第二次到达y轴的时间为:
………2分．
(3)质子再次进入磁场时，速度的方向与电场的方向相同，在洛仑兹力作用下做匀速圆周运动，到达y轴的D点.由几何关系得CD=2Rcos300 ………2分
则质子第二次到达y轴的位置为
………2分
即质子第三次到达y轴的坐标为（0，34.6）. ………1分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com