
题目列表(包括答案和解析)
(14分)已知等比数列![]() 的各项均为正数,且公比不等于1,数列
的各项均为正数,且公比不等于1,数列![]() 对任意正整数n,均有:
对任意正整数n,均有:![]()
成立,又![]() 。
。
(Ⅰ)求数列![]() 的通项公式及前n项和
的通项公式及前n项和![]() ;
;
(Ⅱ)在数列![]() 中依次取出第1项,第2项,第4项,第8项,……,第
中依次取出第1项,第2项,第4项,第8项,……,第![]() 项,……,组成一个新数列
项,……,组成一个新数列![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(Ⅲ)当![]() 时,比较
时,比较![]() 与
与![]() 的大小。
的大小。
已知等比数列![]() 的各项均为正数,且公比不等于1,数列
的各项均为正数,且公比不等于1,数列![]() 对任意正整数n,均有:
对任意正整数n,均有:![]() 成立
成立![]() ;
;
(1)求数列![]() 的通项公式及前n项和
的通项公式及前n项和![]() ;
;
(2)在数列![]() 中依次取出第1项,第2项,第4项,第8项,……,第
中依次取出第1项,第2项,第4项,第8项,……,第![]() 项,……,组成一个新数列
项,……,组成一个新数列![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(3)对(1)(2)中的![]() 、
、![]() ,当
,当![]() 时,比较
时,比较![]() 与
与![]() 的大小。
的大小。
下列各组对象:①2008年北京奥运会上所有的比赛项目;②《高中数学》必修1中的所有难题;③所有质数;4平面上到点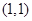 的距离等于
的距离等于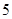 的点的全体;5在数轴上与原点O非常近的点。其中能构成集合的有( )
的点的全体;5在数轴上与原点O非常近的点。其中能构成集合的有( )
A.2组 B.3组 C.4组 D.5组
 的距离等于
的距离等于 的点的全体;5在数轴上与原点O非常近的点。其中能构成集合的有( )
的点的全体;5在数轴上与原点O非常近的点。其中能构成集合的有( )| A.2组 | B.3组 | C.4组 | D.5组 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com