
题目列表(包括答案和解析)
在四棱锥 中,
中, 平面
平面 ,底面
,底面 为矩形,
为矩形, .
.
(Ⅰ)当 时,求证:
时,求证: ;
;
(Ⅱ)若 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.

【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时,底面ABCD为正方形,

又因为 ,
, ………………2分
………………2分
又 ,得证。
,得证。
第二问,建立空间直角坐标系,则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分
设BQ=m,则Q(1,m,0)(0《m《a》
要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得
由此知道a=2, 设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
解:(Ⅰ)当 时,底面ABCD为正方形,
时,底面ABCD为正方形,

又因为 ,
, 又
又
 ………………3分
………………3分
(Ⅱ) 因为AB,AD,AP两两垂直,分别以它们所在直线为X轴、Y轴、Z轴建立坐标系,如图所示,

则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分
设BQ=m,则Q(1,m,0)(0《m《a》要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得 由此知道a=2,
由此知道a=2,
设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC、AD的中点.
(1)求证:DE∥平面PFB;
(2)已知二面角P-BF-C的余弦值为 ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积.

【解析】(1)证:DE//BF即可;
(2)可以利用向量法根据二面角P-BF-C的余弦值为 ,确定高PD的值,即可求出四棱锥的体积.也可利用传统方法直接作出二面角的平面角,求高PD的值也可.在找平面角时,要考虑运用三垂线或逆定理.
,确定高PD的值,即可求出四棱锥的体积.也可利用传统方法直接作出二面角的平面角,求高PD的值也可.在找平面角时,要考虑运用三垂线或逆定理.
如图,已知四棱锥 的底面ABCD为正方形,
的底面ABCD为正方形,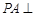 平面ABCD,E、F分别是BC,PC的中点,
平面ABCD,E、F分别是BC,PC的中点, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求二面角 的大小.
的大小.

【解析】第一问利用线面垂直的判定定理和建立空间直角坐标系得到法向量来表示二面角的。

第二问中,以A为原点,如图所示建立直角坐标系
 ,,
,,
设平面FAE法向量为 ,则
,则
 ,
, ,
,

(08年永定一中二模理)我们把平面内与直线的方向向量垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点的轨迹方程的方法,可以求出过点![]() 且法向量为
且法向量为![]() (点法式)方程为
(点法式)方程为![]() ,化简后得
,化简后得![]() .类比以上求法,在空间直角坐标系中,经过点
.类比以上求法,在空间直角坐标系中,经过点![]() ,且法向量为
,且法向量为![]() 的平面(点法式)方程为_______________(请写出化简后的结果).
的平面(点法式)方程为_______________(请写出化简后的结果).
已知直三棱柱 中,
中,  ,
, ,
,
 是
是 和
和 的交点, 若
的交点, 若 .
.
(1)求 的长; (2)求点
的长; (2)求点 到平面
到平面 的距离;
的距离;
(3)求二面角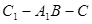 的平面角的正弦值的大小.
的平面角的正弦值的大小.

【解析】本试题主要考查了距离和角的求解运用。第一问中,利用ACC A
A 为正方形,
为正方形,  AC=3
AC=3
第二问中,利用面BB C
C C内作CD
C内作CD BC
BC ,
则CD就是点C平面A
,
则CD就是点C平面A BC
BC 的距离CD=
的距离CD= ,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
解法一: (1)连AC 交A
交A C于E, 易证ACC
C于E, 易证ACC A
A 为正方形,
为正方形,  AC=3
…………… 5分
AC=3
…………… 5分
(2)在面BB C
C C内作CD
C内作CD BC
BC ,
则CD就是点C平面A
,
则CD就是点C平面A BC
BC 的距离CD=
的距离CD= … 8分
… 8分
(3) 易得AC
 面A
面A CB,
过E作EH
CB,
过E作EH A
A B于H, 连HC
B于H, 连HC ,
则HC
,
则HC
 A
A B
B

 C
C HE为二面角C
HE为二面角C -A
-A B-C的平面角. ……… 9分
B-C的平面角. ……… 9分
 sin
sin C
C HE=
HE=
 二面角C
二面角C -A
-A B-C的平面角的正弦大小为
B-C的平面角的正弦大小为 ……… 12分
……… 12分
解法二: (1)分别以直线C B、CC
B、CC 、C
、C A为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C
A为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C (0,
0, 0), B
(0,
0, 0), B (4,
0, 0), B(4, -3, 0), C(0, -3,
0), A
(4,
0, 0), B(4, -3, 0), C(0, -3,
0), A (0,
0, h), A(0, -3, h), G(2, -
(0,
0, h), A(0, -3, h), G(2, - , -
, - ) ……………………… 3分
) ……………………… 3分

 =(2, -
=(2, - , -
, - ),
),  =(0,
-3, -h) ……… 4分
=(0,
-3, -h) ……… 4分

 ·
· =0,
=0,
 h=3
h=3
(2)设平面A BC
BC 得法向量
得法向量 =(a, b, c),则可求得
=(a, b, c),则可求得 =(3, 4, 0) (令a=3)
=(3, 4, 0) (令a=3)
 点A到平面A
点A到平面A BC
BC 的距离为H=|
的距离为H=| |=
|= ……… 8分
……… 8分
(3) 设平面A BC的法向量为
BC的法向量为 =(x, y, z),则可求得
=(x, y, z),则可求得 =(0, 1, 1) (令z=1)
=(0, 1, 1) (令z=1)
 二面角C
二面角C -A
-A B-C的大小
B-C的大小 满足cos
满足cos =
= =
= ………
11分
………
11分
 二面角C
二面角C -A
-A B-C的平面角的正弦大小为
B-C的平面角的正弦大小为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com