
题目列表(包括答案和解析)
a≥-
|
[140,150] | 合计 | |||
| 参加培训 | 5 | 8 | |||
| 未参加培训 | |||||
| 合计 | 4 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

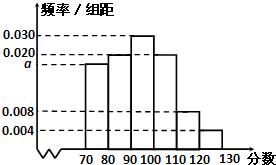 8、高三某班50名学生,在一模数学考试中,成绩全部介于70分与130分之间,将成绩按如下方式分成六组:第一组,成绩大于等于70分且小于80分;第二组,成绩大于等于80分且小于90分;…第六组,成绩大于等于120分且小于等于130分.如图是按上述分组方法得到的频率分布直方图.则90分以下(不含90分)的人数为( )
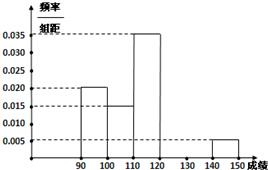
8、高三某班50名学生,在一模数学考试中,成绩全部介于70分与130分之间,将成绩按如下方式分成六组:第一组,成绩大于等于70分且小于80分;第二组,成绩大于等于80分且小于90分;…第六组,成绩大于等于120分且小于等于130分.如图是按上述分组方法得到的频率分布直方图.则90分以下(不含90分)的人数为( )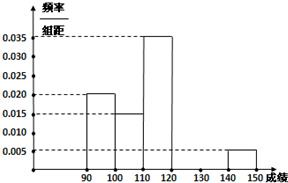 某校高三数学竞赛初赛考试后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
某校高三数学竞赛初赛考试后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.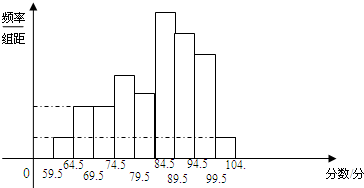 为了了解某校毕业班数学考试情况,抽取了若干名学生的数学成绩,将所得的数据经过整理后,画出频率分布直方图(如图所示).已知从左到右第一组的频率是0.03,第二组的频率是0.06,第四组的频率是0.12,第五组的频率是0.10,第六组的频率是0.27,且第四组的频数是12,则
为了了解某校毕业班数学考试情况,抽取了若干名学生的数学成绩,将所得的数据经过整理后,画出频率分布直方图(如图所示).已知从左到右第一组的频率是0.03,第二组的频率是0.06,第四组的频率是0.12,第五组的频率是0.10,第六组的频率是0.27,且第四组的频数是12,则湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com