题目列表(包括答案和解析)
不等式的基本性质
(1)如果a＞b，那么b＜a；如果b＜a，那么________，即________．
(2)如果a＞b，b＞c，那么________，即a＞b，b＞c
________．
(3)如果a＞b，那么a＋c________b＋c．
(4)如果a＞b，c＞0，那么ac________bc；如果a＞b，c＜0，那么ac________bc．
(5)如果a＞b＞0，那么an________bn(n∈N，n≥2)．
(6)如果________，那么
(n∈N，n≥2)．
利用不等式的基本性质用
“﹥”或“﹤”填空．(1)
如果a﹥b，c﹥d，那么a＋c ________ b＋d；(2)
如果a﹥b﹥0，c﹥d﹥0，那么ac ________ bd _________ 0；(3)a
﹥b﹥0，那么
______
；
(4)a
﹥b﹥0，那么
．
完成答题后，与同学交流体会，并总结一般的规律．
已知函数f(x)＝alnx＋bx,且f(1)＝ －1，f′(1)＝0，
⑴求f(x)；
⑵求f(x)的最大值；
⑶若x＞0,y＞0,证明：lnx＋lny≤
.
本题主要考查函数、导数的基本知识、函数性质的处理以及不等式的综合问题，同时考查考生用函数放缩的方法证明不等式的能力．
若实数
、
、
满足
，则称比远离.
（1）若
比1远离0，求的取值范围；
（2）对任意两个不相等的正数
、
，证明：
比
远离
；
（3）已知函数
的定义域
.任取
，等于
和
中远离0的那个值.写出函数的解析式，并指出它的基本性质（结论不要求证明）.
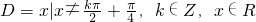．任取x∈D，f（x）等于sinx和cosx中远离0的那个值．写出函数f（x）的解析式，并指出它的基本性质（结论不要求证明）．湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com