
题目列表(包括答案和解析)
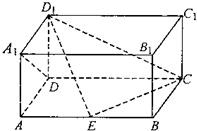 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB>1,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点C1,所爬的最短路程为2
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB>1,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点C1,所爬的最短路程为2| 2 |
| π |
| 4 |
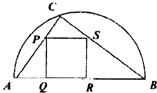 如图,某小区准备绿化一块直径为AB的半圆形空地,点C在半圆弧上,半圆内△ABC外的地方种草,△ABC的内接正方形PQRS内部为一水池,其余地方种花,若AB=2a,∠CAB=θ,设△ABC的面积为S1,正方形PQRS的边长为x,面积为S2,将比值
如图,某小区准备绿化一块直径为AB的半圆形空地,点C在半圆弧上,半圆内△ABC外的地方种草,△ABC的内接正方形PQRS内部为一水池,其余地方种花,若AB=2a,∠CAB=θ,设△ABC的面积为S1,正方形PQRS的边长为x,面积为S2,将比值| S1 |
| S2 |
| 2asin2θ |
| 2+sin2θ |
 如图,已知△ABC中,∠C=
如图,已知△ABC中,∠C=| π |
| 2 |
| T |
| S |
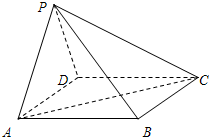 如图,四棱锥P-ABCD的底面为矩形,侧面PAD是正三角形,且侧面PAD⊥底面ABCD
如图,四棱锥P-ABCD的底面为矩形,侧面PAD是正三角形,且侧面PAD⊥底面ABCD| AE |
如图,在长方体![]() 中,
中,![]() ,点
,点![]() 在棱
在棱![]() 上移动,小蚂蚁从点
上移动,小蚂蚁从点![]() 沿长方体的表面经棱
沿长方体的表面经棱![]() 爬到点
爬到点![]() ,所爬的最短路程为
,所爬的最短路程为![]() 。
。
(1)求![]() 的长度;
的长度;
(2)求证:![]() ⊥
⊥![]() ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m ![]()

(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() 。若存在,确定点
。若存在,确定点![]() 的位置;若不存在,请说明理由。
的位置;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com