平面直角坐标系x0y中，动点P到直线x=-2的距离比它到点F（1，0）的距离大1．
（1）求动点P的轨迹C；
（2）求曲线C与直线x=4所围成的区域的面积．

平面上点P与点F（0，1）的距离比它到直线y+2=0的距离小1
（1）求出点P的轨迹方程；
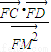（2）过点F作点P的轨迹动弦CD，过C、D两点分别作点P的轨迹的切线，设其交点为M，求点M的轨迹方程，并求出的值．

平面直角坐标系内的向量都可以用一有序实数对唯一表示，这使我们想到可以用向量作为解析几何的研究工具．如图，设直线l的倾斜角为α(α≠90°)．在l上任取两个不同的点，，不妨设向量的方向是向上的，那么向量的坐标是()．过原点作向量，则点P的坐标是()，而且直线OP的倾斜角也是α．根据正切函数的定义得

，

这就是《数学2》中已经得到的斜率公式．上述推导过程比《数学2》中的推导简捷．你能用向量作为工具讨论一下直线的有关问题吗？例如：

(1)过点，平行于向量的直线方程；

(2)向量(A，B)与直线的关系；

(3)设直线和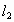的方程分别是

，

，

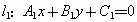
那么，∥，的条件各是什么？如果它们相交，如何得到它们的夹角公式？

(4)点到直线的距离公式如何推导？

在平面直角坐标系xOy中，点P到点F（3，0）的距离的4倍与它到直线x=2的距离的3倍之和记为d，当P点运动时，d恒等于点P的横坐标与18之和
（Ⅰ）求点P的轨迹C；
（Ⅱ）设过点F的直线I与轨迹C相交于M，N两点，求线段MN长度的最大值．