
题目列表(包括答案和解析)
| 1 |
| 2 |
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
| π |
| 4 |
| π |
| 8 |
| 7π |
| 8 |
| π |
| 8 |
| 7π |
| 8 |
我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点A(-3,4),且法向量为 =(1,-2)的直线(点法式)方程为:1×(x+3)+(-2)×(y-4)=0,化简得x-2y+11=0.类比以上方法,在空间直角坐标系o-xyz中,经过点A(1,2,3)且法向量为
=(1,-2)的直线(点法式)方程为:1×(x+3)+(-2)×(y-4)=0,化简得x-2y+11=0.类比以上方法,在空间直角坐标系o-xyz中,经过点A(1,2,3)且法向量为 =(-1,-2,1)的平面的方程为____________ .
=(-1,-2,1)的平面的方程为____________ .
(化简后用关于x,y,z的一般式方程表示)
如下图所示,某畜牧基地要围成相同面积的羊圈4间,一面可利用原有的墙壁,其余各面用篱笆围成,篱笆总长为36m.问每间羊圈的长和宽各为多少时,羊圈面积最大? w.w.w.k.s.5.u.c.o.m ![]()
![]()

已知点 (
( ),过点
),过点 作抛物线
作抛物线 的切线,切点分别为
的切线,切点分别为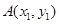 、
、 (其中
(其中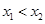 ).
).
(Ⅰ)若 ,求
,求 与
与 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若以点 为圆心的圆
为圆心的圆 与直线
与直线 相切,求圆
相切,求圆 的方程;
的方程;
(Ⅲ)若直线 的方程是
的方程是 ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切,
相切,
求圆 面积的最小值.
面积的最小值.
【解析】本试题主要考查了抛物线的的方程以及性质的运用。直线与圆的位置关系的运用。
中∵直线 与曲线
与曲线 相切,且过点
相切,且过点 ,∴
,∴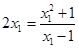 ,利用求根公式得到结论先求直线
,利用求根公式得到结论先求直线 的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
(3)∵直线 的方程是
的方程是 ,
, ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切∴点
相切∴点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即 ,借助于函数的性质圆
,借助于函数的性质圆 面积的最小值
面积的最小值
(Ⅰ)由 可得,
可得, . ------1分
. ------1分
∵直线 与曲线
与曲线 相切,且过点
相切,且过点 ,∴
,∴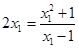 ,即
,即 ,
,
∴ ,或
,或 , --------------------3分
, --------------------3分
同理可得: ,或
,或 ----------------4分
----------------4分
∵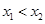 ,∴
,∴ ,
, . -----------------5分
. -----------------5分
(Ⅱ)由(Ⅰ)知, ,
, ,则
,则 的斜率
的斜率 ,
,
∴直线 的方程为:
的方程为: ,又
,又 ,
,
∴ ,即
,即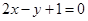 . -----------------7分
. -----------------7分
∵点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即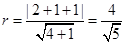 ,--------------8分
,--------------8分
故圆 的面积为
的面积为 . --------------------9分
. --------------------9分
(Ⅲ)∵直线 的方程是
的方程是 ,
, ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切∴点
相切∴点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即 , ………10分
, ………10分
∴
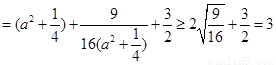 ,
,
当且仅当 ,即
,即 ,
, 时取等号.
时取等号.
故圆 面积的最小值
面积的最小值 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com