给出以下几个命题：
①已知函数f(x)=

x2+4x+2 2

， x＜-1 ，    x≥-1 ．

则f（x）=x有三个根；
②?x₀∈R，x₀≤sinx₀；
③过空间任一点，有且只有一个平面与两异面直线同时平行；
④两条直线l₁：A₁x+B₁y+C₁=0与直线l₂：A₂x+B₂y+C₂=0平行的充要条件是

A1B2=A2B1  B1C2≠B2C1

⑤y=

log 1 2 ( 1 x-1 )

的定义域是[2，+∞）．
则正确的命题有（填序号）．

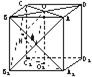如图，在棱长为a的正方体ABCD-A₁B₁C₁D₁中，M、O、O₁分别是A₁B、AC、A₁C₁的中点，且OH⊥O₁B，垂足为H．
（1）求证：MO∥平面BB₁C₁C；
（2）分别求MO与OH的长；
（3）MO与OH是否为异面直线A₁B与AC的公垂线？为什么？求这两条异面直线间的距离．

在空间,关于角和距离,有下列命题:

①平面的斜线与平面所成的角是斜线与平面内所有直线所成角的最小角;

②二面角的平面角是过棱上任意一点在两个面内分别引射线所成的角;

③两条异面直线间的距离是指分别位于这两条直线上的两点间距离的最小值;

④分别位于两个平行平面内的两条直线间的距离等于这两个平面间的距离.

其中正确命题的序号为______________.(把你认为所有正确的命题的序号都填上)

下列命题中正确命题的个数是                                                                                 （　　）

       ①经过空间一点一定可作一平面与两异面直线都平行；

       ②已知平面、，直线a、b，若，，则；

       ③有两个侧面垂直于底面的四棱柱为直四棱柱；

       ④四个侧面两两全等的四棱柱为直四棱柱；

       ⑤底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；

       ⑥底面是等边三角形，∠APB＝∠BPC＝∠CPA，则三棱锥P－ABC是正三棱锥．

       A．0      B．1       C．2       D．3