下列关于正态密度曲线性质的叙述中正确的是

①曲线关于直线x=μ对称,整个曲线在x轴的上方  ②曲线对应的正态总体的概率密度函数是偶函数  ③曲线在x=μ时处于最高点,由这一点向左右两边延伸时,曲线逐渐降低  ④曲线的对称轴位置由μ确定,曲线的形状由σ确定,σ越大曲线越“矮胖”,反过来曲线越“高瘦”

A.①②③             B.①③④           C.②③④            D.①②③④

设函数f（x）=lnx，g（x）=ax+，函数f（x）的图像与x轴的交点也在函数g（x）的图像上，且在此点处f（x）与g（x）有公切线.[来源:学。科。网]

（Ⅰ）求a、b的值； 

（Ⅱ）设x>0，试比较f（x）与g（x）的大小.[来源:学,科,网Z,X,X,K]

【解析】第一问解：因为f（x）=lnx，g（x）=ax+

则其导数为

由题意得，

第二问，由（I）可知，令。

∵，  …………8分

∴是（0，+∞）上的减函数，而F（1）=0，            …………9分

∴当时，，有；当时，，有；当x=1时，，有

解：因为f（x）=lnx，g（x）=ax+

则其导数为

由题意得，

（11）由（I）可知，令。

∵，  …………8分

∴是（0，+∞）上的减函数，而F（1）=0，            …………9分

∴当时，，有；当时，，有；当x=1时，，有

 

设任一正态总体N(μ,σ²)中取值小于x的概率为F(x),标准正态总体N(0,1)中,取值小于x₀ 的概率为Φ(x₀).

(1)证明F(x)可化为Φ(x₀)计算.

(2)利用正态曲线的性质说明:当x取何值时,正态总体N(μ,σ²)相应的函数f(x)=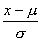(x∈R)有最大值,其最大值是多少？

过曲线f(x)=x³上两点P(1,1)和Q(1+Δx,1+Δy)作曲线的割线,求当Δx=0.1时割线的斜率.

下列关于正态曲线性质的叙述正确的是__________.(填入你认为正确的序号)

①曲线关于直线x=μ对称,这个曲线只在x轴上方

②曲线关于直线x=σ对称,这个曲线只有当x∈(-3σ，3σ)时才在x轴上方

③曲线关于y轴对称，因为曲线对应的正态密度函数是一个偶函数

④曲线在x=μ时处于最高点，由这一点向左右两边延伸时，曲线逐渐降低

⑤曲线的对称轴由μ确定，曲线的形状由σ确定

⑥σ越大，曲线越“矮胖”，总体分布越分散；σ越小，曲线越“高”,总体分布越集中