练习册

  • 练习册
  • 试题
    ③无理函数或形如这类函数.如取自然对数之后可变形为.对两边求导可得.高中数学第十五章 复数考试内容: 复数的概念． 复数的加法和减法． 复数的乘法和除法． 数系的扩充．考试要求:(1)了解复数的有关概念及复数的代数表示和几何意义．(2)掌握复数代数形式的运算法则.能进行复数代数形式的加法.减法.乘法.除法运算．(3)了解从自然数系到复数系的关系及扩充的基本思想． 【查看更多】

     

    题目列表(包括答案和解析)

    （2012•葫芦岛模拟）我们常用以下方法求形如y=f（x）g（x）的函数的导数：先两边同取自然对数得：lny=g（x）lnf（x），再两边同时求导得到：
    1
    y
    •y′=g′（x）lnf（x）+g（x）•
    1
    f(x)
    •f′（x），于是得到：y′=f（x）g（x）[g′（x）lnf（x）+g（x）•
    1
    f(x)
    •f′（x）]，运用此方法求得函数y=x
    1
    x
    的一个单调递增区间是（　　）

    查看答案和解析>>

    （2012•江苏二模）若函数f（x）在（0，+∞）上恒有xf′（x）＞f（x）成立（其中f′（x）为f（x）的导函数），则称这类函数为A类函数．
    （1）若函数g（x）=x2-1，试判断g（x）是否为A类函数；
    （2）若函数h(x)=ax-3-lnx-
    1-ax
    是A类函数，求函数h（x）的单调区间；
    （3）若函数f（x）是A类函数，当x1＞0，x2＞0时，证明f（x1）+f（x2）＜f（x1+x2）．

    查看答案和解析>>

    求形如的函数的导数，我们常采用以下做法：先两边同取自然对数得：,再两边同时求导得，于是得到：，运用此方法求得函数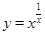的一个单调递增区间是(    )

    A．         B．         C．         D．

     

    查看答案和解析>>

    我们常用以下方法求形如y=f（x）g（x）的函数的导数：先两边同取自然对数得：lny=g（x）lnf（x），再两边同时求导得到：•y′=g′（x）lnf（x）+g（x）••f′（x），于是得到：y′=f（x）g（x）[g′（x）lnf（x）+g（x）••f′（x）]，运用此方法求得函数y=的一个单调递增区间是（ ）
    A．（e，4）
    B．（3，6）
    C．（0，e）
    D．（2，3）

    查看答案和解析>>

    对于 函数，则它是周期函数，这类函数的最小正周期是               

    （    ）

        A．             B．             C．             D．

    查看答案和解析>>


    同步练习册答案