
题目列表(包括答案和解析)
已知定义在 上的函数
上的函数 ,其中
,其中 为常数.
为常数.
(1)当 是函数
是函数 的一个极值点,求
的一个极值点,求 的值;
的值;
(2)若函数 在区间
在区间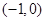 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)当 时,若
时,若 ,在
,在 处取得最大值,求实数
处取得最大值,求实数 的取值范围.
的取值范围.
已知定义在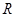 上的函数
上的函数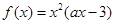 ,其中
,其中 为常数.
为常数.
(1)当 是函数
是函数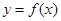 的一个极值点,求
的一个极值点,求 的值;
的值;
(2)若函数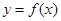 在区间
在区间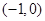 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)当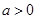 时,若
时,若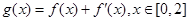 ,在
,在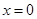 处取得最大值,求实数
处取得最大值,求实数 的取值范围.
的取值范围.
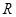 上的函数
上的函数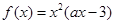 ,其中
,其中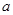 为常数.
为常数.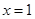 是函数
是函数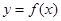 的一个极值点,求
的一个极值点,求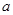 的值;
的值;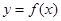 在区间
在区间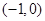 上是增函数,求实数
上是增函数,求实数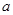 的取值范围;
的取值范围;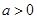 时,若
时,若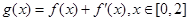 ,在
,在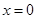 处取得最大值,求实数
处取得最大值,求实数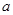 的取值范围.
的取值范围.已知定义在![]() 上的函数
上的函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)若![]() 是函数
是函数![]() 的一个极值点,求
的一个极值点,求![]() 的值.
的值.
(2)若函数![]() 在区间
在区间![]() 上是增函数,求
上是增函数,求![]() 的取值范围.
的取值范围.
(3)若函数![]() 在
在![]() 处取得最大值,求正数
处取得最大值,求正数![]() 的取值范围.
的取值范围.
已知定义在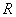 上的函数
上的函数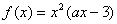 ,其中
,其中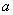 为常数。
为常数。
(I)若当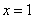 时,函数
时,函数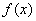 取得极值,求
取得极值,求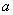 的值;
的值;
(II)若函数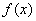 在区间(-1,0)上是增函数,求
在区间(-1,0)上是增函数,求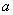 的取值范围;
的取值范围;
(III)若函数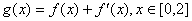 ,在
,在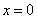 处取得最大值,求正数
处取得最大值,求正数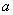 的取值范围。
的取值范围。
2009.3
一、选择题
(1)B (2)A (3)B (4)C (5)B (6)D
(7)D (8)C (9)C (10)B (11)A (12)C
二、填空题
|