练习册

  • 练习册
  • 试题
    10．已知的解集是 【查看更多】

     

    题目列表(包括答案和解析)

    已知数学公式的解集，若CRA是?RB的必要不充分条件；
    求：
    （Ⅰ）集合A，B；　　　　　　　　　　
    （Ⅱ）实数m的取值范围．

    查看答案和解析>>

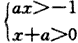    已知的解集不是空集，则实数a的取值范围是（    ）。

    查看答案和解析>>

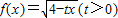    已知的定义域为A，不等式x2-4x-12＜0的解集为B．记p：x∈A，q：x∈B
    （1）当t=2时，试判断p是q的什么条件？
    （2）若p是q的必要不充分条件，求实数t的取值范围．

    查看答案和解析>>

    已知集合M是同时满足下列两个性质的函数f（x）的全体：
    ①函数f（x）在其定义域上是单调函数；
    ②在函数f（x）的定义域内存在闭区间[a，b]使得f（x）在[a，b]上的最小值是
    a
    2
    ，且最大值是
    b
    2
    ．请解答以下问题
    （1）判断函数f(x)=x+
    2
    x
    (x∈(0，+∞))    是否属于集合M？并说明理由；
    （2）判断函数g（x）=-x3是否属于集合M？并说明理由．若是，请找出满足②的闭区间[a，b]；
    （3）若函数h(x)=
    		x-1
    +t∈M    ，求实数t的取值范围．

    查看答案和解析>>

    已知函数f（x）满足2f（x+2）=f（x），当x∈(0，2)时，f(x)=lnx+ax(a＜-
    1
    2
    )    ，当x∈（-4，-2）时，f（x）的最大值为-4．
    （1）求x∈（0，2）时函数f（x）的解析式；
    （2）是否存在实数b使得不等式
    x-b
    f(x)+x
    ＞
    		x
    对于x∈（0，1）∪（1，2）时恒成立，若存在，求出实数b的取值集合，若不存在，说明理由．

    查看答案和解析>>

     

    1.A    2.B    3.C    4.C    5.A    6.C   7.D    8.D   9.A   10.C

    11.80    12.30    13.c    14.   15. .

    三、解答题

    16．解：（1）(ka+b)2=3(a－kb)2   k2++2ka?b=3(1+k2－2ka?b)

    ∴a?b=  当k=1时取等号.                                （6分）

       （2）a?b=

           

            ∴时，a?b=取最大值1.                                                               （12分）

    17．解：（1）由已知有xn+1－1=2(xn－1)

    ∴{xn－1}是以1为首项以2为公比的等比数列，又x1=2.

    ∴xn－1=2n－1   ∴xn=1+2n－1(n∈N*)                                                             （6分）

       （2）由

    又当n∈N*时，xn≥2故点（xn，yn）在射线x+y=3（xn≥2）上。                （12分）

    18．解：（1）记乙胜为事件A，则P（A）=

       （2）解法一：由题意：(x，y)=（1，4）或（1，3）

    或（1，2）或（1，1）或（2，3）或（2，2）

    或（2，1）或（3，2）或（3，1）或（4，1）。

    故当x=1，y=4时，x+2y取最大值9，即x=1，

    y=4时乙获胜的概率最大为.（12分）

    解法二：令t=x+2y，，（x,y）取值如图所示，由

    线性规划知识知x=1,y=4时，t最大，

    故x=1，y=4，乙获胜的概率最大为.                                                   （12分）

    19．解（1）设正三棱柱―的侧棱长为．取中点，连．

    是正三角形，．

    又底面侧面，且交线为．

    侧面．……3分

    连，则直线与侧面所成的角为．

    在中，，解得．

    此正三棱柱的侧棱长为．                       ……5分

    （2）过作于，连，

    侧面．为二面角的平面角．…7分

    在中，，

    又，．

    又在中，．

    故二面角的大小为．         ……9分

    （3）解法1：由（2）可知，平面,平面平面，且交线为，

    过作于，则平面．……11分

    在中，．

    为中点，点到平面的距离为．  ………… 13

    20．解：

     

    21．解：（1）

    ∴，故椭圆Qn的焦距2cn≥1.                                                            （4分）

       （2）（i）设Pn(xn，yn)，则

            

     

     

     

     

     

     


    同步练习册答案