练习册

  • 练习册
  • 试题
    14．如图.已知平面人的向 量.满足: 【查看更多】

     

    题目列表(包括答案和解析)

    精英家教网如图，已知等腰△ABC的底边BC=3，顶角为120°，D是BC边上一点，且BD=1．把△ADC沿AD折起，使得平面CAD⊥平面ABD，连接BC形成三棱锥C-ABD．
    （Ⅰ） ①求证：AC⊥平面ABD；②求三棱锥C-ABD的体积；
    （Ⅱ） 求AC与平面BCD所成的角的正弦值．

    查看答案和解析>>

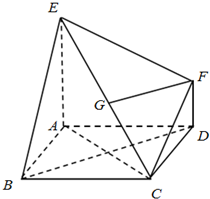    如图，已知多面体EABCDF的底面ABCD是正方形，EA⊥底面ABCD，FD∥EA，且EA=2FD．
    （1）求证：CB⊥平面ABE；
    （2）连接AC，BD交于点O，取EC中点G．证明：FG∥平面ABCD．

    查看答案和解析>>

    （2012•石景山区一模）如图，已知平面α∩β=l，A、B是l上的两个点，C、D在平面β内，且DA⊥α，CB⊥α，AD=4，AB=6，BC=8，在平面α上有一个动点P，使得∠APD=∠BPC，则△PAB面积的最大值是（　　）

    查看答案和解析>>

    （2004•河西区一模）如图，已知平面α⊥平面β，α∩β=AB，点C∈α，点D∈β，且AB=AC=BC=2
    		3
    ，E为BC的中点，AC⊥BD，BD=6．
    （Ⅰ）求证：BD⊥平面α；
    （Ⅱ）求证：平面AED⊥平面BCD；
    （Ⅲ）求三棱锥C-AED的体积．

    查看答案和解析>>

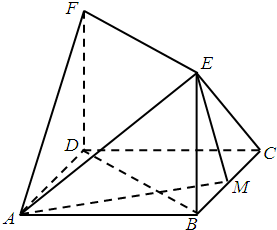    精英家教网如图，已知正方形ABCD的边长为1，FD⊥平面ABCD，EB⊥平面ABCD，FD=BE=1，M为BC边上的动点．
    （1）证明：ME∥平面FAD；
    （2）试探究点M的位置，使平面AME⊥平面AEF．

    查看答案和解析>>

     

    1.A    2.B    3.C    4.C    5.A    6.C   7.D    8.D   9.A   10.C

    11.80    12.30    13.c    14.   15. .

    三、解答题

    16．解：（1）(ka+b)2=3(a－kb)2   k2++2ka?b=3(1+k2－2ka?b)

    ∴a?b=  当k=1时取等号.                                （6分）

       （2）a?b=

           

            ∴时，a?b=取最大值1.                                                               （12分）

    17．解：（1）由已知有xn+1－1=2(xn－1)

    ∴{xn－1}是以1为首项以2为公比的等比数列，又x1=2.

    ∴xn－1=2n－1   ∴xn=1+2n－1(n∈N*)                                                             （6分）

       （2）由

    又当n∈N*时，xn≥2故点（xn，yn）在射线x+y=3（xn≥2）上。                （12分）

    18．解：（1）记乙胜为事件A，则P（A）=

       （2）解法一：由题意：(x，y)=（1，4）或（1，3）

    或（1，2）或（1，1）或（2，3）或（2，2）

    或（2，1）或（3，2）或（3，1）或（4，1）。

    故当x=1，y=4时，x+2y取最大值9，即x=1，

    y=4时乙获胜的概率最大为.（12分）

    解法二：令t=x+2y，，（x,y）取值如图所示，由

    线性规划知识知x=1,y=4时，t最大，

    故x=1，y=4，乙获胜的概率最大为.                                                   （12分）

    19．解（1）设正三棱柱―的侧棱长为．取中点，连．

    是正三角形，．

    又底面侧面，且交线为．

    侧面．……3分

    连，则直线与侧面所成的角为．

    在中，，解得．

    此正三棱柱的侧棱长为．                       ……5分

    （2）过作于，连，

    侧面．为二面角的平面角．…7分

    在中，，

    又，．

    又在中，．

    故二面角的大小为．         ……9分

    （3）解法1：由（2）可知，平面,平面平面，且交线为，

    过作于，则平面．……11分

    在中，．

    为中点，点到平面的距离为．  ………… 13

    20．解：

     

    21．解：（1）

    ∴，故椭圆Qn的焦距2cn≥1.                                                            （4分）

       （2）（i）设Pn(xn，yn)，则

            

     

     

     

     

     

     


    同步练习册答案