
题目列表(包括答案和解析)
(本小题满分12分)一个袋中有8个大小相同的小球,其中红球1个,白球和黑球若干,现从袋中有放回地取球,每次随机取一个,又知连续取两次都是白球的概率为![]() :
:
(1)求该口袋内白球和黑球的个数;
(2)若取一个红球记2分,取一个白球记1分,取一个黑球记0 分,连续取三次分数之和为4分的概率;
(3)现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取、乙后取,然后甲再取,直到两个小朋友中有1人取得黑球时游戏终止,每个球在每一次被取出的机会均相同.求当游戏终止时,取球次数不多于3的概率。
(本小题满分12分)
某甲有一个放有3个红球、2个白球、1个黄球共6个球的箱子;某乙也有一个放有3个红球、2个白球、1个黄球共6个球的箱子.
(Ⅰ)若甲在自己的箱子里任意取球,取后不放回,每次只取一个球,直到取到红球为止,求甲取球次数![]() 的数学期望;
的数学期望;
(Ⅱ)若甲、乙两人各从自己的箱子里任取一球比颜色,规定同色时为甲胜,异色时为乙胜,这个游戏规则公平吗?请说明理由.
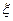 的数学期望;
的数学期望;
1.A 2.B 3.C 4.C 5.A 6.C 7.D 8.D 9.A 10.C
11.80 12.30 13.c 14. --数学文科.files/image083.gif) 15.
15. --数学文科.files/image085.gif) .
.
三、解答题
16.解:(1)(ka+b)2=3(a-kb)2 k2++2ka?b=3(1+k2-2ka?b)
∴a?b=--数学文科.files/image087.gif) 当k=1时取等号. (6分)
当k=1时取等号. (6分)
(2)a?b=--数学文科.files/image089.gif)
--数学文科.files/image091.gif)
∴--数学文科.files/image093.gif) 时,a?b=取最大值1. (12分)
时,a?b=取最大值1. (12分)
17.解:(1)由已知有xn+1-1=2(xn-1)
∴{xn-1}是以1为首项以2为公比的等比数列,又x1=2.
∴xn-1=2n-1 ∴xn=1+2n-1(n∈N*) (6分)
(2)由--数学文科.files/image095.gif)
又当n∈N*时,xn≥2故点(xn,yn)在射线x+y=3(xn≥2)上。 (12分)
18.解:(1)记乙胜为事件A,则P(A)=--数学文科.files/image097.gif)
|