
题目列表(包括答案和解析)
(本题满分13分)
已知数列![]() 满足
满足![]() ,
,![]()
(1)计算![]() 的值;
的值;
(2)由(1)的结果猜想![]() 的通项公式,并证明你的结论。
的通项公式,并证明你的结论。
(本题满分13分)
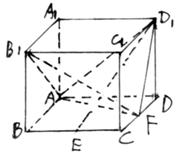
如图在棱长为2的正方体![]() 中,点F为棱CD中点,点E在棱BC上
中,点F为棱CD中点,点E在棱BC上
(1)确定点E位置使![]() 面
面![]() ;
;
(2)当![]() 面
面![]() 时,求二面角
时,求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(本题满分13分)
一个口袋里有4个不同的红球,6个不同的白球(球的大小均一样)
(1)从中任取3个球,恰好为同色球的不同取法有多少种?
(2)取得一个红球记为2分,一个白球记为1分。从口袋中取出五个球,使总分不小于7分的不同取法共有多少种?(本题满分13分)已知定义域为[0,1]的函数![]() 同时满足: ①对于任意的
同时满足: ①对于任意的![]() ,总有
,总有![]() ; ②
; ②![]() =1; ③当
=1; ③当![]() 时有
时有![]() .
.
(1)求![]() 的值;w.w.w.k.s.5.u.c.o.m
的值;w.w.w.k.s.5.u.c.o.m
(2)求![]() 的最大值;
的最大值;
(3)当对于任意![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
(本题满分13分)
已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,过
两点,过![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,且
两点,且![]() ,垂足为
,垂足为![]() .
.
(1)设![]() 点的坐标为
点的坐标为![]() ,求
,求![]() 的最值;
的最值;
(2)求四边形![]() 的面积的最小值.
的面积的最小值.
1.A 2.B 3.C 4.C 5.A 6.C 7.D 8.D 9.A 10.C
11.80 12.30 13.c 14. --数学文科.files/image083.gif) 15.
15. --数学文科.files/image085.gif) .
.
三、解答题
16.解:(1)(ka+b)2=3(a-kb)2 k2++2ka?b=3(1+k2-2ka?b)
∴a?b=--数学文科.files/image087.gif) 当k=1时取等号. (6分)
当k=1时取等号. (6分)
(2)a?b=--数学文科.files/image089.gif)
--数学文科.files/image091.gif)
∴--数学文科.files/image093.gif) 时,a?b=取最大值1. (12分)
时,a?b=取最大值1. (12分)
17.解:(1)由已知有xn+1-1=2(xn-1)
∴{xn-1}是以1为首项以2为公比的等比数列,又x1=2.
∴xn-1=2n-1 ∴xn=1+2n-1(n∈N*) (6分)
(2)由--数学文科.files/image095.gif)
又当n∈N*时,xn≥2故点(xn,yn)在射线x+y=3(xn≥2)上。 (12分)
18.解:(1)记乙胜为事件A,则P(A)=--数学文科.files/image097.gif)
|