
题目列表(包括答案和解析)
| x |
| 3 |
已知函数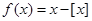 ,其中
,其中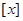 表示不超过实数
表示不超过实数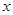 的最大整数.若关于
的最大整数.若关于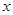 的方程
的方程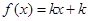 有三个不同的实根,则实数
有三个不同的实根,则实数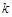 的取值范围是( )
的取值范围是( )
(A)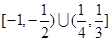 (B)
(B)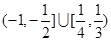
(C)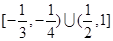 (D)
(D)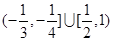
已知函数 ,其中
,其中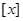 表示不超过实数
表示不超过实数 的最大整数.若关于
的最大整数.若关于 的方程
的方程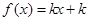 有三个不同的实根,则实数
有三个不同的实根,则实数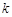 的取值范围是( )
的取值范围是( )
A.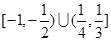 | B.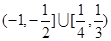 |
C.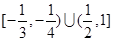 | D.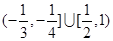 |
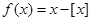 ,其中
,其中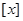 表示不超过实数
表示不超过实数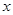 的最大整数.若关于
的最大整数.若关于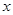 的方程
的方程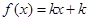 有三个不同的实根,则实数
有三个不同的实根,则实数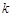 的取值范围是( )
的取值范围是( )A.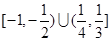 | B.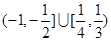 |
C.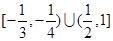 | D.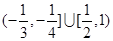 |
| C | f(1) n |
| C | f(2) n |
| C | f(3) n |
| C | f(2n) n |
一、BDCBD ACA CC
二、--数学文科.files/image253.gif)
--数学文科.files/image255.gif)
--数学文科.files/image257.gif)
--数学文科.files/image259.gif) ①④
①④
三、--数学文科.files/image261.jpg) 16.解:(1)
16.解:(1)--数学文科.files/image263.gif)
--数学文科.files/image265.gif)
--数学文科.files/image261.jpg)
--数学文科.files/image267.gif) 即
即 --数学文科.files/image269.gif)
又--数学文科.files/image271.gif) 为锐角
为锐角 --数学文科.files/image273.gif)
--数学文科.files/image275.gif)
--数学文科.files/image277.gif)
(2)--数学文科.files/image279.gif)
--数学文科.files/image281.gif)
--数学文科.files/image283.gif)
又--数学文科.files/image285.gif) 代入上式得:
代入上式得:--数学文科.files/image287.gif) (当且仅当
(当且仅当 --数学文科.files/image289.gif) 时等号成立。)
时等号成立。)
--数学文科.files/image291.gif) (当且仅当
(当且仅当 --数学文科.files/image289.gif) 时等号成立。)
时等号成立。)
17.解:(1)由已知得--数学文科.files/image293.gif) 解得
解得--数学文科.files/image295.gif) .设数列
.设数列--数学文科.files/image170.gif) 的公比为
的公比为--数学文科.files/image298.gif) ,
,
由--数学文科.files/image295.gif) ,可得
,可得--数学文科.files/image301.gif) .又
.又--数学文科.files/image177.gif) ,可知
,可知--数学文科.files/image304.gif) ,即
,即--数学文科.files/image306.gif) ,
,
解得--数学文科.files/image308.gif) . 由题意得
. 由题意得--数学文科.files/image310.gif) .
. --数学文科.files/image312.gif) .故数列
.故数列--数学文科.files/image170.gif) 的通项为
的通项为--数学文科.files/image315.gif) .
.
(2)由于--数学文科.files/image182.gif) 由(1)得
由(1)得--数学文科.files/image318.gif)
--数学文科.files/image320.gif)
--数学文科.files/image322.gif) =
=--数学文科.files/image324.gif)
18.解:(1)因为--数学文科.files/image195.gif) 图象的一条对称轴是直线
图象的一条对称轴是直线--数学文科.files/image191.gif)
--数学文科.files/image328.gif)
|