练习册

  • 练习册
  • 试题
    即 得证. 【查看更多】

     

    题目列表(包括答案和解析)

    证明不是直接从原命题的条件逐步推得命题成立，这种不直接证明的方法通常称为________．如反证法，反证法的证明过程概括为：“________”“________”“________”“________”，

    即从否定结论开始，经过正确的推理，导致逻辑矛盾，从而达到新的否定(即肯定原命题)的过程．

    查看答案和解析>>

    在证明恒等式时，可利用组合数表示n2，即推得．类似地，在推导恒等式时，也可以利用组合数表示n3推得．则n3=    ．

    查看答案和解析>>

    某同学在证明命题“
    		7
    -
    		3
    ＜
    		6
    -
    		2
    ”时作了如下分析，请你补充完整．
    要证明
    		7
    -
    		3
    ＜
    		6
    -
    		2
    ，只需证明
    		7
    +
    		2
    ＜
    		6
    +
    		3
    		7
    +
    		2
    ＜
    		6
    +
    		3
    ，只需证明
    (
    		7
    +
    		2
    )2＜(
    		6
    +
    		3
    )2
    (
    		7
    +
    		2
    )2＜(
    		6
    +
    		3
    )2
    ，
    展开得9+2
    		14
    ＜9+2
    		18
    ，即
    		14
    ＜
    		18
    ，只需证明14＜18，
    因为14＜18显然成立
    因为14＜18显然成立
    ，
    所以原不等式：
    		7
    +
    		2
    ＜
    		6
    +
    		3
    成立．

    查看答案和解析>>

    通过计算可得下列等式：

    22－12＝2×1＋1，

    32－22＝2×2＋1，

    42－32＝2×3＋1，

    ……

    (n＋1)2－n2＝2×n＋1，

    将以上各式分别相加，得

    (n＋1)2－12＝2×(1＋2＋3＋…＋n)＋n，

    即1＋2＋3＋…＋n＝．

    类比上述方法，请你证明12＋22＋32＋…＋n2＝n(n＋1)(2n＋1)．

    查看答案和解析>>

    用数学归纳法证明：

    ．

    【解析】首先证明当n=1时等式成立，再假设n=k时等式成立，得到等式

    ，

    下面证明当n=k+1时等式左边

    ，

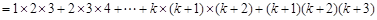    根据前面的假设化简即可得到结果，最后得到结论．

     

    查看答案和解析>>

    一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有 一项是符合题目要求的。

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    答案

     

     

     

     

     

     

     

     

     

     

    二、填空题：（本大题共5个小题，每小题5分，共25分，）

    11．    12.     13.    14.       15.

     

    三、解答题：


    同步练习册答案