查看答案和解析>>

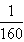某西部山区的某种特产由于运输的原因，长期只能在当地销售．一直以来，当地政府通过投资对该项特产的销售进行扶持，已知：在当地销售，每投入x万元，可获得纯利润P=-(x-40)²+100万元(已扣除投资，下同)。当地政府拟在新的十年发展规划中加快发展此特产的销售，其规划方案为：在未来10年内对该项目每年都投入60万元的销售资金，其中在前5年中，每年都从60万元中拨出30万元用于修建一条公路。公路5年建成，通车前该特产只能在当地销售；公路通车后的5年中，该特产既在本地销售，也在外地销售．在外地销售的投资收益为：每投入x万元，可获纯利润Q=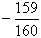(60-x)²+(60-x)万元，问仅从这10年的累积利润看，该规划方案是否可行？

查看答案和解析>>

查看答案和解析>>

一、选择题：1-5  BABAC       6-10  DAACC

二、填空题：11．625     12．     13．

14．     15．    

三、解答题：本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤．

16．（本小题满分12分）

解：（1）由题意知

的夹角           

（2）

有最小值

的最小值是

17．（本小题满分12分）

（1）证法一：在中，是等腰直角的中位线，                                       

在四棱锥中，，， 平面，                         

又平面,                                            

证法二：同证法一      平面，                                                   

又平面,                                   

（2）在直角梯形中，,                     

又垂直平分，                      

∴                              

三棱锥的体积为  

18．（本小题满分14分）

解：，   

因为函数在处的切线斜率为-3，

所以，即

又得

（1）函数在时有极值，所以

解得

所以．

（2）因为函数在区间上单调递增，所以导函数

在区间上的值恒大于或等于零

则得，所以实数的取值范围为

19．（本小题满分14分）

解：（1）由题设知

由于，则有，所以点的坐标为

故所在直线方程为

所以坐标原点到直线的距离为

又，所以  解得：

所求椭圆的方程为

（2）由题意可知直线的斜率存在，设直线斜率为

直线的方程为，则有

设，由于、、三点共线，且

根据题意得,解得或

又在椭圆上，故或

解得,综上，直线的斜率为或

20．（本小题满分14分）

解: 在实施规划前, 由题设(万元),

知每年只须投入40万, 即可获得最大利润100万元.

则10年的总利润为W₁=100×10=1000（万元）.

实施规划后的前5年中, 由题设知,

每年投入30万元时, 有最大利润(万元).

所以前5年的利润和为(万元). 

设在公路通车的后5年中, 每年用x万元投资于本地的销售, 而用剩下的（60－x）万元于外地区的销售投资, 则其总利润为：

.

当x=30时，W₂|_max=4950（万元）.

从而 ,   该规划方案有极大实施价值.

21．（本小题满分14分）

解：（1）设

,又

（2）由已知得

两式相减得,

当.若

（3）由,

.

若

可知,.