
题目列表(包括答案和解析)
已知函数![]() ,
,![]() 。
。
(Ⅰ)求![]() 在区间
在区间![]() 的最小值;
的最小值;
(Ⅱ)求证:若![]() ,则不等式
,则不等式![]() ≥
≥![]() 对于任意的
对于任意的![]() 恒成立;
恒成立;
(Ⅲ)求证:若![]() ,则不等式
,则不等式![]() ≥
≥![]() 对于任意
对于任意![]() 的
的![]()
![]() 恒成立。
恒成立。
已知函数![]() 在区间[m,n]上为增函数,
在区间[m,n]上为增函数,
(Ⅰ)若m=0,n=1时,求实数a的取值范围;
(Ⅱ)若f(m)f(n)=-4.则当f(n)-f(m)取最小值时,
(ⅰ)求实数a的值;
(ⅱ)若P(x1,y1),Q(x2,y2)(a<x1<x2<n)是f(x)图象上的两点,且存在实数x0=(a,n)使得![]() ,证明:x1<x0<x2.
,证明:x1<x0<x2.
| x+1 |
| 3π |
| 4 |
| 2 |
| 3π |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
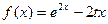 ,
,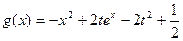 。
。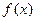 在区间
在区间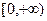 的最小值;
的最小值;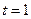 ,则不等式
,则不等式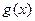 ≥
≥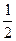 对于任意的
对于任意的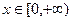 恒成立;
恒成立;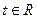 ,则不等式
,则不等式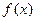 ≥
≥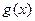 对于任意
对于任意 的
的
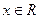 恒成立。
恒成立。(本小题满分12分)已知函数![]() ,
,![]() .
.
(1)求![]() 在区间
在区间![]() 的最小值; (2)求证:若
的最小值; (2)求证:若![]() ,则不等式
,则不等式![]() ≥
≥![]() 对于任意的
对于任意的![]() 恒成立; (3)求证:若
恒成立; (3)求证:若![]() ,则不等式
,则不等式![]() ≥
≥![]() 对于任意的
对于任意的![]() 恒成立.
恒成立.
一、选择题:本大题共10小题,每小题5分,共50分.
CBCDB DADCA
二、填空题:本大题共5小题,每小题5分,共25分.
11.90 12.[.files/image245.gif) ) 13.
) 13..files/image247.gif) 14.1 ;3899 15.
14.1 ;3899 15..files/image249.gif)
三、解答题:本大题共6小题,共75分.
16.(本小题满分13分)
解:(1).files/image130.gif)
.files/image154.gif)
.files/image251.gif)
.files/image253.gif) ……3分
……3分.files/image255.gif) ……4分
……4分
令.files/image257.gif)
.files/image259.gif)
.files/image261.gif) 的单调区间
的单调区间.files/image263.gif) ,k∈Z ......6分
,k∈Z ......6分
(2)由.files/image265.gif) 得
得 .files/image267.gif)
.files/image269.gif) .....7分
.....7分
又.files/image271.gif) 为
为.files/image092.gif) 的内角
的内角.files/image274.gif)
.files/image276.gif)
.files/image278.gif) ......9分
......9分
.files/image280.gif)
.files/image282.gif)
.files/image284.gif) ...11分
...11分
.files/image286.gif)
.files/image288.gif) ....12分
....12分
17. (本小题满分13分)
解:(1)记“甲击中目标的次数减去乙击中目标的次数为
.files/image290.gif) ,解得
,解得.files/image292.gif) .....4分
.....4分
(2).files/image174.gif) 的所有可能取值为0,1,2.记“在第一次射击中甲击中目标”为事件
的所有可能取值为0,1,2.记“在第一次射击中甲击中目标”为事件.files/image294.gif) ;记“在第一次射击中乙击中目标”为事件
;记“在第一次射击中乙击中目标”为事件.files/image296.gif) .
.
则.files/image298.gif) ,
,
.files/image300.gif)
.files/image302.gif) ,.....10分
,.....10分
所以.files/image174.gif) 的分布列为
的分布列为
.files/image174.gif)
0
1
2
P
.files/image306.gif)
.files/image168.gif)
.files/image309.gif)
∴.files/image311.gif) =
=.files/image313.gif) .....12分
.....12分
18. (本小题满分13分)
解:(1)当.files/image191.gif) 为
为.files/image193.gif) 中点时,有
中点时,有.files/image196.gif) 平面
平面.files/image198.gif)
证明:连结.files/image315.gif) 交
交.files/image317.gif) 于
于.files/image319.gif) ,连结
,连结.files/image321.gif)
∵四边形.files/image187.gif) 是矩形 ∴
是矩形 ∴.files/image319.gif) 为
为.files/image315.gif) 中点
中点
又.files/image191.gif) 为
为.files/image193.gif) 中点,从而
中点,从而.files/image323.gif)
∵.files/image325.gif) 平面
平面.files/image198.gif) ,
,.files/image327.gif) 平面
平面.files/image198.gif)
∴.files/image196.gif) 平面
平面.files/image198.gif) .....4分
.....4分
(2)建立空间直角坐标系.files/image329.gif) 如图所示,
如图所示,
则.files/image331.gif) ,
,.files/image333.gif) ,
,.files/image335.gif) ,
,.files/image337.gif) ,
,.files/image339.gif)
.....6分
所以.files/image341.gif) ,
,.files/image343.gif) .
.
设.files/image345.gif) 为平面
为平面.files/image198.gif) 的法向量,则有
的法向量,则有.files/image347.gif) ,即
,即.files/image349.gif)
令.files/image351.gif) ,可得平面
,可得平面.files/image198.gif) 的一个法向量为
的一个法向量为.files/image353.gif) ,.....9分
,.....9分
而平面.files/image355.gif) 的一个法向量为
的一个法向量为.files/image357.gif) .....10分
.....10分
所以.files/image359.gif)
所以二面角.files/image201.gif) 的余弦值为
的余弦值为.files/image361.gif) .....12分
.....12分
(用其它方法解题酌情给分)
19.(本小题满分12分)
解:(1)由题意知.files/image363.gif)
.files/image365.gif)
因此数列.files/image205.gif) 是一个首项
是一个首项.files/image368.gif) .公比为3的等比数列,所以
.公比为3的等比数列,所以.files/image370.gif) ......2分
......2分
.files/image372.gif) 又
又.files/image374.gif)
.files/image376.gif) =100―(1+3+9)
=100―(1+3+9)
所以.files/image378.gif) =87,解得
=87,解得.files/image380.gif)
因此数列.files/image207.gif) 是一个首项
是一个首项.files/image383.gif) ,公差为―5的等差数列,
,公差为―5的等差数列,
所以 .files/image385.gif) .....4分
.....4分
(2) 求视力不小于5.0的学生人数为.files/image387.gif) .....7分
.....7分
(3) 由.files/image389.gif) ①
①
可知,当.files/image391.gif) 时,
时,.files/image393.gif) ②
②
①-②得,当.files/image391.gif) 时,
时,.files/image395.gif) , www.zxsx.com
, www.zxsx.com
.files/image397.gif) ,
.....11分
,
.....11分
又.files/image399.gif)
因此数列.files/image212.gif) 是一个从第2项开始的公比为3的等比数列,
是一个从第2项开始的公比为3的等比数列,
数列.files/image212.gif) 的通项公式为
的通项公式为.files/image402.gif) .....13分
.....13分
20.(本小题满分12分)
解:(1)由于.files/image219.gif) ,
,
∴.files/image404.gif) ,解得
,解得.files/image406.gif) ,
,
∴椭圆的方程是.files/image408.gif) .....3分
.....3分
(2)∵.files/image221.gif) ,∴
,∴.files/image410.gif) 三点共线,
三点共线,
而.files/image412.gif) ,设直线的方程为
,设直线的方程为.files/image414.gif) ,
,
由.files/image416.gif) 消去
消去.files/image012.gif) 得:
得: .files/image419.gif)
由.files/image421.gif) ,解得
,解得.files/image423.gif) .....6分
.....6分
设.files/image425.gif) ,由韦达定理得
,由韦达定理得.files/image427.gif) ①,
①,
又由.files/image221.gif) 得:
得:.files/image429.gif) ,∴
,∴.files/image431.gif) ②.
②.
将②式代入①式得:.files/image433.gif) ,
,
消去.files/image435.gif) 得:
得:.files/image437.gif) .....10分
.....10分
设.files/image439.gif) ,当
,当.files/image223.gif) 时,
时, .files/image441.gif) 是减函数,
是减函数,
∴.files/image443.gif) , ∴
, ∴.files/image445.gif) , www.zxsx.com
, www.zxsx.com
解得.files/image447.gif) ,又由
,又由.files/image423.gif) 得
得.files/image449.gif) ,
,
∴直线AB的斜率的取值范围是.files/image451.gif) .....13分
.....13分
21. (本小题满分12分)
(1)解:.files/image453.gif)
①若.files/image455.gif)
∵.files/image126.gif) ,则
,则.files/image458.gif) ,∴
,∴.files/image460.gif) ,即
,即.files/image462.gif) .
.
∴.files/image130.gif) 在区间
在区间.files/image230.gif) 是增函数,故
是增函数,故.files/image130.gif) 在区间
在区间.files/image230.gif) 的最小值是
的最小值是.files/image464.gif)
.....2分
②若.files/image466.gif)
令.files/image468.gif) ,得
,得.files/image470.gif) .
.
又当.files/image472.gif) 时,
时,.files/image474.gif) ;当
;当.files/image476.gif) 时,
时,.files/image478.gif) ,
,
∴.files/image130.gif) 在区间
在区间.files/image230.gif) 的最小值是
的最小值是.files/image480.gif) .....4分
.....4分
(2)证明:当.files/image482.gif) 时,
时,.files/image484.gif) ,则
,则.files/image486.gif) ,
,
∴.files/image488.gif) ,
,
当.files/image237.gif) 时,有
时,有.files/image490.gif) ,∴
,∴.files/image492.gif) 在
在.files/image230.gif) 内是增函数,
内是增函数,
∴.files/image495.gif) ,
,
∴.files/image234.gif) 在
在.files/image230.gif) 内是增函数,www.zxsx.com
内是增函数,www.zxsx.com
∴对于任意的.files/image237.gif) ,
,.files/image498.gif) 恒成立.....7分
恒成立.....7分
(3)证明:.files/image500.gif)
.files/image502.gif) ,
,
令.files/image504.gif)
则当.files/image239.gif) 时,
时,.files/image506.gif) ≥
≥.files/image508.gif)
.files/image510.gif) ,.....10分
,.....10分
令.files/image512.gif) ,则
,则.files/image514.gif) ,www.zxsx.com
,www.zxsx.com
当.files/image516.gif) 时,
时, .files/image518.gif) ;当
;当.files/image520.gif) 时,
时,.files/image522.gif) ;当
;当.files/image524.gif) 时,
时,.files/image526.gif) ,
,
则.files/image512.gif) 在
在.files/image528.gif) 是减函数,在
是减函数,在.files/image530.gif) 是增函数,
是增函数,
∴.files/image532.gif) ,
,
∴.files/image534.gif) ,
,
∴.files/image536.gif) ,即不等式
,即不等式.files/image130.gif) ≥
≥.files/image234.gif) 对于任意的
对于任意的.files/image243.gif) 恒成立.....13分
恒成立.....13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com