
题目列表(包括答案和解析)
(本小题满分14分)
某市一家庭今年一月份、二月份和三月份煤气用量和支付费用如下表所示:
|
月份 |
用气量(立方米) |
煤气费(元) |
|
1 |
4 |
4.00 |
|
2 |
25 |
14.00 |
|
3 |
35 |
19.00 |
该市煤气收费的方法是:煤气费=基本费十超额费十保险费.
若每月用气量不超过最低额度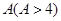 立方米时,只付基本费
立方米时,只付基本费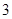 元和每户每月定额保险费
元和每户每月定额保险费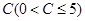 元;若用气量超过
元;若用气量超过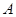 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付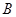 元.
元.
(1)根据上面的表格求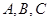 的值;
的值;
(2)记用户第四月份用气为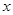 立方米,求他应交的煤气费
立方米,求他应交的煤气费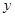 (元).
(元).
(本小题满分14分)
某市一家庭今年一月份、二月份和三月份煤气用量和支付费用如下表所示:
| 月份 | 用气量(立方米) | 煤气费(元) |
| 1 | 4 | 4.00 |
| 2 | 25 | 14.00 |
| 3 | 35 | 19.00 |
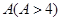 立方米时,只付基本费
立方米时,只付基本费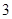 元和每户每月定额保险费
元和每户每月定额保险费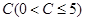 元;若用气量超过
元;若用气量超过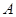 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付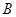 元.
元.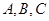 的值;
的值;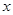 立方米,求他应交的煤气费
立方米,求他应交的煤气费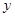 (元).
(元).(本小题满分12分)
第8届中学生模拟联合国大会将在本校举行,为了搞好接待工作,组委会招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如下茎叶图(单位:cm):

 男 女
男 女
 15
7 7 8 9 9 9
15
7 7 8 9 9 9
9 8 16 0 0 1 2 4 5 8 9
8 6 5 0 17 2 5 6
7 4 2 1 18 0
1 0 19
若男生身高在180cm以上(包括180cm)定义为“高个子”, 在180cm以下(不包括180cm)定义为“非高个子”, 女生身高在170cm以上(包括170cm)定义为“高个子”,在170cm以下(不包括170cm)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取6人,则应分别抽取“高个子”、“非高个子”各几人?
(2)从(1)中抽出的6人中选2人担任领座员,那么至少有一人是“高个子”的概率是多少?
(本小题满分12分)
第8届中学生模拟联合国大会将在本校举行,为了搞好接待工作,组委会招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如下茎叶图(单位:cm):
 男 女
男 女 15 7 7 8 9 9 9
15 7 7 8 9 9 9
9 8 16 0 0 1 2 4 5 8 9
8 6 5 0 17 2 5 6
7 4 2 1 18 0
1 0 19
若男生身高在180cm以上(包括180cm)定义为“高个子”, 在180cm以下(不包括180cm)定义为“非高个子”, 女生身高在170cm以上(包括170cm)定义为“高个子”,在170cm以下(不包括170cm)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取6人,则应分别抽取“高个子”、“非高个子”各几人?
(2)从(1)中抽出的6人中选2人担任领座员,那么至少有一人是“高个子”的概率是多少?
 男 女
男 女 15 7 7 8 9 9 9
15 7 7 8 9 9 9
一、填空题 (每题5分)
1)2009.03.files/image134.gif) 2)
2)2009.03.files/image136.gif) 3)0 4)
3)0 4) 2009.03.files/image138.gif) 5)
5)2009.03.files/image140.gif) 6)
6) 2009.03.files/image142.gif) 7)②④ 8)
7)②④ 8)2009.03.files/image144.gif) 9)
9)2009.03.files/image146.gif) 10)
10)2009.03.files/image148.gif) 11)7
11)7
二、选择题(每题5分)
2009.03.files/image089.jpg) 12、A 13、B 14、D 15、D
12、A 13、B 14、D 15、D
三、解答题
16、16、
(1)因为2009.03.files/image150.gif) ,所以∠BCA(或其补角)即为异面直线
,所以∠BCA(或其补角)即为异面直线2009.03.files/image152.gif) 与
与2009.03.files/image154.gif) 所成角
-------(3分)
所成角
-------(3分)
∠ABC=90°, AB=BC=1,所以2009.03.files/image156.gif) , -------(2分)
, -------(2分)
即异面直线2009.03.files/image152.gif) 与
与2009.03.files/image154.gif) 所成角大小为
所成角大小为2009.03.files/image024.gif) 。
-------(1分)
。
-------(1分)
(2)直三棱柱ABC-A1B2009.03.files/image159.gif) ,所以
,所以2009.03.files/image161.gif) 即为直线A
即为直线A2009.03.files/image163.gif) 。 -------(2分)
。 -------(2分)
2009.03.files/image165.gif) 中,AB=BC=1得到
中,AB=BC=1得到2009.03.files/image167.gif) ,
,2009.03.files/image169.gif) 中,得到
中,得到2009.03.files/image171.gif) , -------(2分)
, -------(2分)
所以2009.03.files/image173.gif) -------(2分)
-------(2分)
17、2009.03.files/image175.gif) -------(1分)
-------(1分)
=2009.03.files/image177.gif) -------(1分)
-------(1分)
=2009.03.files/image179.gif) -------(1分)
-------(1分)
若2009.03.files/image095.gif) 为其图象对称中心的横坐标,即
为其图象对称中心的横坐标,即2009.03.files/image182.gif) =0, -------(1分)
=0, -------(1分)
2009.03.files/image184.gif) , -------(1分)
, -------(1分)
解得:2009.03.files/image186.gif) -------(1分)
-------(1分)
(2)2009.03.files/image188.gif) , -------(2分)
, -------(2分)
即2009.03.files/image190.gif) ,而
,而2009.03.files/image192.gif) ,所以
,所以2009.03.files/image194.gif) 。
-------(2分)
。
-------(2分)
2009.03.files/image196.gif) ,
,2009.03.files/image198.gif) , -------(2分)
, -------(2分)
所以2009.03.files/image200.gif) ------(2分)
------(2分)
18、2009.03.files/image202.gif) ,顾客得到的优惠率是
,顾客得到的优惠率是2009.03.files/image204.gif) 。 -------(5分)
。 -------(5分)
(2)、设商品的标价为x元,则500≤x≤800 ----- -(2分)
消费金额: 400≤0.8x≤640
由题意可得:
(1)2009.03.files/image205.jpg) ≥
≥2009.03.files/image206.jpg) 无解
------(3分)
无解
------(3分)
或(2)2009.03.files/image207.jpg) ≥
≥2009.03.files/image206.jpg) 得:625≤x≤750 ------(3分)
得:625≤x≤750 ------(3分)
因此,当顾客购买标价在2009.03.files/image208.jpg) 元内的商品时,可得到不小于
元内的商品时,可得到不小于2009.03.files/image206.jpg) 的优惠率。------(1分)
的优惠率。------(1分)
19、(1)y=2009.03.files/image209.jpg) ?
?2009.03.files/image210.jpg) =(2x-b)+(b+1)=2x+1
-----(1分)
=(2x-b)+(b+1)=2x+1
-----(1分)
2009.03.files/image212.gif) 与
与2009.03.files/image095.gif) 轴的交点
轴的交点2009.03.files/image215.gif) 为
为2009.03.files/image217.gif) ,所以
,所以2009.03.files/image219.gif) ;
-----(1分)
;
-----(1分)
所以2009.03.files/image221.gif) ,即
,即2009.03.files/image223.gif) ,
-----(1分)
,
-----(1分)
因为2009.03.files/image225.gif) 在
在2009.03.files/image212.gif) 上,所以
上,所以2009.03.files/image227.gif) ,即
,即2009.03.files/image229.gif) -----(1分)
-----(1分)
(2)设2009.03.files/image231.gif)
2009.03.files/image233.gif) (
(2009.03.files/image235.gif) ),
),
即2009.03.files/image237.gif)
2009.03.files/image233.gif) (
(2009.03.files/image235.gif) ) ----(1分)
) ----(1分)
(A)当2009.03.files/image241.gif) 时,
时,2009.03.files/image243.gif)
2009.03.files/image245.gif) ----(1分)
----(1分)
=2009.03.files/image247.gif) =
=2009.03.files/image249.gif) ,而
,而2009.03.files/image251.gif) ,所以
,所以2009.03.files/image253.gif) ----(1分)
----(1分)
(B)当2009.03.files/image255.gif) 时,
时,2009.03.files/image257.gif) ----(1分)
----(1分)
= 2009.03.files/image259.gif) =
=2009.03.files/image261.gif) ,
----(1分)
,
----(1分)
而2009.03.files/image263.gif) ,所以
,所以2009.03.files/image265.gif) ----(1分)
----(1分)
因此2009.03.files/image267.gif) (
(2009.03.files/image235.gif) )
----(1分)
)
----(1分)
(3)假设2009.03.files/image126.gif) ,使得
,使得2009.03.files/image128.gif) ,
,
(A)2009.03.files/image269.gif) 为奇数
为奇数
(一)2009.03.files/image130.gif) 为奇数,则
为奇数,则2009.03.files/image272.gif) 为偶数。则
为偶数。则2009.03.files/image274.gif) ,
,2009.03.files/image276.gif) 。则
。则2009.03.files/image278.gif) ,解得:
,解得:2009.03.files/image280.gif) 与
与2009.03.files/image235.gif) 矛盾。
----(1分)
矛盾。
----(1分)
(二)2009.03.files/image130.gif) 为偶数,则
为偶数,则2009.03.files/image272.gif) 为奇数。则
为奇数。则2009.03.files/image283.gif) ,
,2009.03.files/image285.gif) 。则
。则2009.03.files/image287.gif) ,解得:
,解得:2009.03.files/image289.gif) (
(2009.03.files/image291.gif) 是正偶数)。 ----(1分)
是正偶数)。 ----(1分)
(B)2009.03.files/image269.gif) 为偶数
为偶数
(一)2009.03.files/image130.gif) 为奇数,则
为奇数,则2009.03.files/image272.gif) 为奇数。则
为奇数。则2009.03.files/image274.gif) ,
,2009.03.files/image285.gif) 。则
。则2009.03.files/image294.gif) ,解得:
,解得:2009.03.files/image296.gif) (
(2009.03.files/image298.gif) 是正奇数)。
----(1分)
是正奇数)。
----(1分)
(二)2009.03.files/image130.gif) 为偶数,则
为偶数,则2009.03.files/image272.gif) 为偶数。则
为偶数。则2009.03.files/image283.gif) ,
,2009.03.files/image276.gif) 。则
。则2009.03.files/image301.gif) ,解得:
,解得:2009.03.files/image303.gif) 与
与2009.03.files/image235.gif) 矛盾。 ----(1分)
矛盾。 ----(1分)
由此得:对于给定常数m(2009.03.files/image124.gif) ),这样的
),这样的2009.03.files/image130.gif) 总存在;当
总存在;当2009.03.files/image269.gif) 是奇数时,
是奇数时,2009.03.files/image289.gif) ;当
;当2009.03.files/image269.gif) 是偶数时,
是偶数时,2009.03.files/image296.gif) 。
----(1分)
。
----(1分)
20、(1)解法(A):点P与点F(2,0)的距离比它到直线2009.03.files/image095.gif) +4=0的距离小2,所以点P与点F(2,0)的距离与它到直线
+4=0的距离小2,所以点P与点F(2,0)的距离与它到直线2009.03.files/image095.gif) +2=0的距离相等。 ----(1分)
+2=0的距离相等。 ----(1分)
由抛物线定义得:点2009.03.files/image309.gif) 在以
在以2009.03.files/image311.gif) 为焦点直线
为焦点直线2009.03.files/image095.gif) +2=0为准线的抛物线上, ----(1分)
+2=0为准线的抛物线上, ----(1分)
抛物线方程为2009.03.files/image313.gif) 。 ----(2分)
。 ----(2分)
解法(B):设动点2009.03.files/image315.gif) ,则
,则2009.03.files/image317.gif) 。当
。当2009.03.files/image319.gif) 时,
时,2009.03.files/image321.gif) ,化简得:
,化简得:2009.03.files/image323.gif) ,显然
,显然2009.03.files/image325.gif) ,而
,而2009.03.files/image319.gif) ,此时曲线不存在。当
,此时曲线不存在。当2009.03.files/image136.gif) 时,
时,2009.03.files/image328.gif) ,化简得:
,化简得:2009.03.files/image313.gif) 。
。
(2)2009.03.files/image330.gif) ,
,
2009.03.files/image332.gif) ,
,
2009.03.files/image334.gif) ,
----(1分)
,
----(1分)
2009.03.files/image336.gif) ,
,
2009.03.files/image338.gif) ,即
,即2009.03.files/image340.gif) ,
,2009.03.files/image342.gif) ,
----(2分)
,
----(2分)
直线为2009.03.files/image344.gif) ,所以
,所以2009.03.files/image346.gif) ----(1分)
----(1分)
2009.03.files/image348.gif)
2009.03.files/image350.gif) ----(1分)
----(1分)
由(a)(b)得:直线恒过定点2009.03.files/image352.gif) 。
----(1分)
。
----(1分)
1、(逆命题)如果直线2009.03.files/image346.gif) ,且与抛物线
,且与抛物线2009.03.files/image313.gif) 相交于A、B两点,O为坐标原点。求证:OA⊥OB (评分:提出问题得1分,解答正确得1分)
相交于A、B两点,O为坐标原点。求证:OA⊥OB (评分:提出问题得1分,解答正确得1分)
(若,求证:2009.03.files/image353.jpg) ?
?2009.03.files/image354.jpg) =0,得分相同)
=0,得分相同)
2、(简单推广命题)如果直线L与抛物线2009.03.files/image355.jpg) =2px(p>0)相交于A、B两点,且OA⊥OB。求证:直线L过定点(2p,0)
=2px(p>0)相交于A、B两点,且OA⊥OB。求证:直线L过定点(2p,0)
或:它的逆命题(评分:提出问题得2分,解答正确得1分)
3、(类比)
3.1(1)如果直线L与椭圆2009.03.files/image356.jpg) +
+2009.03.files/image357.jpg) =1(a>b>0)相交于A、B两点,M是其右顶点,当MA⊥MB。求证:直线L过定点(
=1(a>b>0)相交于A、B两点,M是其右顶点,当MA⊥MB。求证:直线L过定点(2009.03.files/image358.jpg) ,0)
,0)
3.1(2)如果直线L与椭圆2009.03.files/image356.jpg) +
+2009.03.files/image357.jpg) =1(a>b>0)相交于A、B两点,M是其左顶点,当MA⊥MB。求证:直线L过定点(
=1(a>b>0)相交于A、B两点,M是其左顶点,当MA⊥MB。求证:直线L过定点(2009.03.files/image359.jpg) ,0)
,0)
3.1(3)或它的逆命题
3.2(1)如果直线L与双曲线2009.03.files/image360.jpg) -
-2009.03.files/image361.jpg) =1(a>0,b>0)相交于A、B两点,M是其右顶点,当MA⊥MB。求证:直线L过定点(
=1(a>0,b>0)相交于A、B两点,M是其右顶点,当MA⊥MB。求证:直线L过定点(2009.03.files/image362.jpg) ,0)(a≠b)
,0)(a≠b)
3.2(2)如果直线L与双曲线2009.03.files/image360.jpg) -
-2009.03.files/image361.jpg) =1(a>0,b>0)相交于A、B两点,M是其左顶点,当MA⊥MB。求证:直线L过定点(
=1(a>0,b>0)相交于A、B两点,M是其左顶点,当MA⊥MB。求证:直线L过定点(2009.03.files/image363.jpg) ,0)(a≠b)
,0)(a≠b)
3.2(3)或它的逆命题
(评分:提出问题得3分,解答正确得3分)
4、(再推广)
直角顶点在圆锥曲线上运动
如:如果直线L与抛物线2009.03.files/image355.jpg) =2px(p>0)相交于A、B两点,P是抛物线上一定点(
=2px(p>0)相交于A、B两点,P是抛物线上一定点(2009.03.files/image364.jpg) ,
,2009.03.files/image365.jpg) ),且PA⊥PB。求证:直线L过定点(
),且PA⊥PB。求证:直线L过定点(2009.03.files/image364.jpg) +2p,-
+2p,-2009.03.files/image365.jpg) )
)
(评分:提出问题得4分,解答正确得3分)
5、(再推广)
如果直线L与抛物线2009.03.files/image355.jpg) =2px(p>0)相交于A、B两点,P是抛物线上一定点(
=2px(p>0)相交于A、B两点,P是抛物线上一定点(2009.03.files/image364.jpg) ,
,2009.03.files/image365.jpg) ),PA与PB的斜率乘积是常数m。求证:直线L过定点(
),PA与PB的斜率乘积是常数m。求证:直线L过定点(2009.03.files/image364.jpg) -
-2009.03.files/image366.jpg) ,-
,-2009.03.files/image365.jpg) )
)
(评分:提出问题得5分,解答正确得4分)
或2009.03.files/image367.jpg) ?
?2009.03.files/image368.jpg) 为常数
为常数
顶点在圆锥曲线上运动并把直角改为一般定角或OA与OB的斜率乘积是常数或2009.03.files/image353.jpg) ?
?2009.03.files/image354.jpg) 为常数
为常数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com