
题目列表(包括答案和解析)
(22) (本小题满分14分)
如图,椭圆![]() (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.

(本小题12分)
已知某商品的价格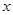 (元)与需求量
(元)与需求量 (件)之间的关系有如下一组数据:
(件)之间的关系有如下一组数据:
|
|
14 |
16 |
18 |
20 |
22 |
|
|
12 |
10 |
7 |
5 |
3 |
(1)画出 关于
关于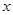 的散点图
的散点图
(2)用最小二乘法求出回归直线方程
(3)计算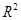 的值,并说明回归模型拟合程度的好坏。
的值,并说明回归模型拟合程度的好坏。
(本小题12分)
已知某商品的价格 (元)与需求量
(元)与需求量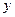 (件)之间的关系有如下一组数据:
(件)之间的关系有如下一组数据:
 | 14 | 16 | 18 | 20 | 22 |
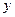 | 12 | 10 | 7 | 5 | 3 |
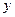 关于
关于 的散点图
的散点图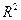 的值,并说明回归模型拟合程度的好坏。
的值,并说明回归模型拟合程度的好坏。(本小题满分14分)
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(Ⅰ)求选取的2组数据恰好是相邻两个月的概率;(5分)
(Ⅱ)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程![]() ;(6分)
;(6分)
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?(3分)
(参考公式: 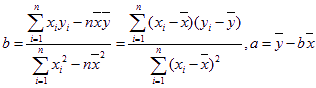 )
)
(本小题满分12分)在第9届校园文化艺术节棋类比赛项目报名过程中,我校高二(2)班共有16名男生和14名女生预报名参加,调查发现,男、女选手中分别有10人和6人会围棋.
(I)根据以上数据完成以下2 2列联表:
2列联表:
|
|
会围棋 |
不会围棋 |
总计 |
|
男 |
|
|
|
|
女 |
|
|
|
|
总计 |
|
|
30 |
并回答能否在犯错的概率不超过0.10的前提下认为性别与会围棋有关?
参考公式: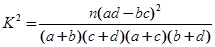 其中n=a+b+c+d
其中n=a+b+c+d
参考数据:
|
|
0.40 |
0.25 |
0.10 |
0.010 |
|
|
0.708 |
1.323 |
2.706 |
6.635 |
(Ⅱ)若从会围棋的选手中随机抽取3人成立该班围棋代表队,则该代表队中既有男又
有女的概率是多少?
(Ⅲ)若从14名女棋手中随机抽取2人参加棋类比赛,记会围棋的人数为 ,求
,求 的期望.
的期望.
一、1 B 2 D 3 A 4 D 5 C 6 B
7 A 8 A 9 C 10 D 11 C 12 B
二、13、3 14、.files/image216.gif) 15、-160 16、
15、-160 16、 .files/image218.gif)
三、17、解: (1).files/image220.gif)
.files/image002.gif) ……… 3分
……… 3分
.files/image222.gif)
.files/image152.gif) 的最小正周期为
的最小正周期为.files/image041.gif)
.files/image002.gif) …………………
5分
…………………
5分
(2).files/image002.gif)
.files/image225.gif) , ………………… 7分
, ………………… 7分
.files/image227.gif) …………………
10分
…………………
10分
.files/image222.gif)
.files/image229.gif)
.files/image002.gif) ………………… 11分
………………… 11分
.files/image222.gif) 当
当.files/image154.gif) 时,函数
时,函数.files/image152.gif) 的最大值为1,最小值
的最大值为1,最小值.files/image231.gif)
.files/image002.gif) ……… 12分
……… 12分
18.解:(1)P1=.files/image233.gif) ;
……… 6分
;
……… 6分
(2)方法一:P2=.files/image235.gif)
方法二:P2=.files/image237.gif)
方法三:P2=1-.files/image239.gif) ……… 12分
……… 12分
19、解法一:
(Ⅰ)连结.files/image162.gif) C交BC
C交BC.files/image242.gif) 于O,则O是B
于O,则O是B .files/image244.gif) C的中点,连结DO。
C的中点,连结DO。
.files/image246.jpg) ∵在△A
∵在△A.files/image248.gif) C中,O、D均为中点,
C中,O、D均为中点,
∴A.files/image248.gif) ∥DO…………………………2分
∥DO…………………………2分
∵A.files/image248.gif)
.files/image250.gif) 平面B
平面B.files/image158.gif) D,DO
D,DO.files/image253.gif) 平面B
平面B.files/image158.gif) D,
D,
∴A.files/image248.gif) ∥平面B
∥平面B.files/image158.gif) D。…………………4分
D。…………………4分
(Ⅱ)设正三棱柱底面边长为2,则DC = 1。
∵∠.files/image158.gif) DC = 60°,∴C
DC = 60°,∴C.files/image158.gif) =
= .files/image255.gif) 。
。
作DE⊥BC于E。
∵平面BC.files/image158.gif) ⊥平面ABC,
⊥平面ABC,
∴DE⊥平面BC.files/image158.gif)
.files/image248.gif)
作EF⊥B.files/image158.gif) 于F,连结DF,则 DF⊥B
于F,连结DF,则 DF⊥B.files/image158.gif)
∴∠DFE是二面角D-B.files/image158.gif) -C的平面角………………8分
-C的平面角………………8分
在Rt△DEC中,DE=.files/image259.gif)
在Rt△BFE中,EF =
BE?sin.files/image261.gif)
∴在Rt△DEF中,tan∠DFE = .files/image263.gif)
.files/image265.gif) ∴二面角D-B
∴二面角D-B.files/image158.gif) -C的大小为arctan
-C的大小为arctan.files/image268.gif) ………………12分
………………12分
解法二:以AC的中D为原点建立坐标系,如图,
设| AD | = 1∵∠.files/image158.gif) DC =60°∴| C
DC =60°∴| C.files/image158.gif) |
=
|
= .files/image255.gif) 。
。
则A(1,0,0),B(0,.files/image255.gif) ,0),C(-1,0,0),
,0),C(-1,0,0),
.files/image273.gif) (1,0
(1,0.files/image255.gif) ),
),.files/image276.gif) ,
,.files/image278.gif)
(Ⅰ)连结.files/image248.gif) C交B
C交B.files/image281.gif) 于O是
于O是.files/image248.gif) C的中点,连结DO,则
C的中点,连结DO,则
O.files/image284.gif) .
. .files/image286.gif) =
=.files/image288.gif)
∵A.files/image248.gif)
.files/image250.gif) 平面B
平面B.files/image281.gif) D,
D,
∴A.files/image248.gif) ∥平面B
∥平面B.files/image281.gif) D.………………………………………………4分
D.………………………………………………4分
(Ⅱ).files/image294.gif) =(-1,0,
=(-1,0,.files/image255.gif) ),
),.files/image297.gif)
设平面B.files/image281.gif) D的法向量为n = ( x , y , z ),则
D的法向量为n = ( x , y , z ),则.files/image300.gif)
即.files/image302.gif) 则有
则有.files/image304.gif) = 0令z = 1
= 0令z = 1
则n = (.files/image255.gif) ,0,1)
…………………………………8分
,0,1)
…………………………………8分
设平面BC.files/image158.gif)
.files/image248.gif) 的法向量为m = ( x′
,y′,z′)
的法向量为m = ( x′
,y′,z′)
|