
题目列表(包括答案和解析)
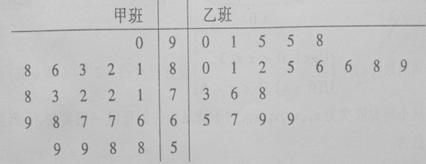
某电视台举办了“中华好声音”大型歌手选秀活动,过程分为初赛、复赛和决赛,经初赛进入复赛的40名选手被平均分成甲、乙两个班,由组委会聘请两位导师各负责一个班进行声乐培训。下面是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图:

赛制规定:参加复赛的40名选手中,获得的支持票数排在前5名的选手可进入决赛,若第5名出现并列,则一起进入决赛;另外,票数不低于95票的选手在决赛时拥有“优先挑战权”。
1、从进入决赛的选手中随机抽出3名,求其中恰有1名拥有“优先挑战权”的概率;
2、电视台决定,复赛票数不低于85票的选手将成为电视台的“签约歌手”,请填写下面的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成为‘签约歌手’与选择的导师有关?
|
|
甲班 |
乙班 |
合计 |
|
签约歌手 |
|
|
|
|
末签约歌手 |
|
|
|
|
合计 |
|
|
|
下面临界值表仅供参考:
|
P(K2≥k) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
k |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
参考公式:K2= ,其中
,其中
某电视台举办了“中华好声音”大型歌手选秀活动,过程分为初赛、复赛和决赛,经初赛进入复赛的40名选手被平均分成甲、乙两个班,由组委会聘请两位导师各负责一个班进行声乐培训。下面是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图: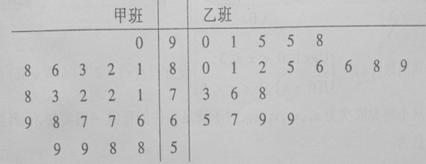
赛制规定:参加复赛的40名选手中,获得的支持票数排在前5名的选手可进入决赛,若第5名出现并列,则一起进入决赛;另外,票数不低于95票的选手在决赛时拥有“优先挑战权”。
1、从进入决赛的选手中随机抽出3名,求其中恰有1名拥有“优先挑战权”的概率;
2、电视台决定,复赛票数不低于85票的选手将成为电视台的“签约歌手”,请填写下面的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成为‘签约歌手’与选择的导师有关?
| | 甲班 | 乙班 | 合计 |
| 签约歌手 | | | |
| 末签约歌手 | | | |
| 合计 | | | |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
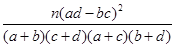 ,其中
,其中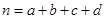
| | 甲班 | 乙班 | 合计 |
| 签约歌手 | | | |
| 末签约歌手 | | | |
| 合计 | | | |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中
在本次数学期中考试试卷中共有10道选择题,每道选择题有4个选项,其中只有一个是正确的。评分标准规定:“每题只选一项,答对得5分,不答或答错得0分”.某考生每道题都给出一个答案, 且已确定有7道题的答案是正确的,而其余题中,有1道题可判断出两个选项是错误的,有一道可以判断出一个选项是错误的,还有一道因不了解题意只能乱猜。试求出该考生:
(1)选择题得满分(50分)的概率;
(2)选择题所得分数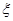 的数学期望。
的数学期望。
【解析】第一问总利用独立事件的概率乘法公式得分为50分,10道题必须全做对.在其余的3道题中,有1道题答对的概率为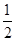 ,有1道题答对的概率为
,有1道题答对的概率为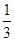 ,还有1道答对的概率为
,还有1道答对的概率为 ,
,
所以得分为50分的概率为: 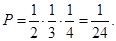
第二问中,依题意,该考生得分的范围为{35,40,45,50}
得分为35分表示只做对了7道题,其余各题都做错,
所以概率为
得分为40分的概率为:
同理求得,得分为45分的概率为:
得分为50分的概率为:
得到分布列和期望值。
解:(1)得分为50分,10道题必须全做对.在其余的3道题中,有1道题答对的概率为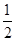 ,有1道题答对的概率为
,有1道题答对的概率为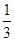 ,还有1道答对的概率为
,还有1道答对的概率为 ,
,
所以得分为50分的概率为: 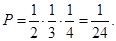 …………5分
…………5分
(2)依题意,该考生得分的范围为{35,40,45,50} …………6分
得分为35分表示只做对了7道题,其余各题都做错,
所以概率为 …………7分
…………7分
得分为40分的概率为: …………8分
…………8分
同理求得,得分为45分的概率为: …………9分
…………9分
得分为50分的概率为: …………10分
…………10分
所以得分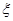 的分布列为
的分布列为
|
|
35 |
40 |
45 |
50 |
|
|
|
|
|
|
数学期望
一、选择题:本大题共8个小题,每小题5分,共40分。
题号
1
2
3
4
5
6
7
8
答案
B
A
B
D
C
D
C
B
二、填空题:本大题共6个小题,每小题5分,共30分
9.60%20数学理科.files/image224.gif) 10. 4 11.
10. 4 11. %20数学理科.files/image226.gif) 12. 2 13.
12. 2 13.%20数学理科.files/image228.gif) 与
与%20数学理科.files/image230.gif) 或
或 %20数学理科.files/image232.gif) 与
与%20数学理科.files/image234.gif) 14. -2;1
14. -2;1
三、解答题: 本大题共6个小题,共80分。
15. (本小题共13分)已知函数%20数学理科.files/image236.gif)
(Ⅰ)求函数%20数学理科.files/image051.gif) 的定义域; (Ⅱ)求函数
的定义域; (Ⅱ)求函数%20数学理科.files/image051.gif) 在区间
在区间%20数学理科.files/image128.gif) 上的最值。
上的最值。
解:(Ⅰ)由题意 %20数学理科.files/image238.gif)
%20数学理科.files/image240.gif)
%20数学理科.files/image242.gif)
%20数学理科.files/image240.gif)
%20数学理科.files/image245.gif)
所求定义域为
{%20数学理科.files/image247.gif) }
…………4分
}
…………4分
(Ⅱ)%20数学理科.files/image249.gif)
%20数学理科.files/image251.gif)
%20数学理科.files/image253.gif)
%20数学理科.files/image255.gif) …………9分
…………9分
由%20数学理科.files/image257.gif) 知
知 %20数学理科.files/image259.gif) ,
,
所以当%20数学理科.files/image261.gif) 时,
时,%20数学理科.files/image051.gif) 取得最大值为
取得最大值为%20数学理科.files/image263.gif) ;
…………11分
;
…………11分
当%20数学理科.files/image265.gif) 时,
时,%20数学理科.files/image051.gif) 取得最小值为0 。
…………13分
取得最小值为0 。
…………13分
16.(本小题共13分)已知数列%20数学理科.files/image078.gif) 中,
中,%20数学理科.files/image130.gif) ,当
,当%20数学理科.files/image132.gif) 时,函数
时,函数%20数学理科.files/image134.gif) 取得极值。(Ⅰ)求数列
取得极值。(Ⅰ)求数列%20数学理科.files/image136.gif) 的通项;(Ⅱ)在数列
的通项;(Ⅱ)在数列%20数学理科.files/image138.gif) 中,
中,%20数学理科.files/image140.gif) ,
,%20数学理科.files/image142.gif) ,求
,求%20数学理科.files/image144.gif) 的值
的值
解:(Ⅰ) %20数学理科.files/image267.gif) 由题意
由题意%20数学理科.files/image269.gif) 得
得 %20数学理科.files/image271.gif) , …………6分
, …………6分
又%20数学理科.files/image273.gif)
%20数学理科.files/image275.gif) 所以 数列
所以 数列%20数学理科.files/image136.gif) 是公比为
是公比为%20数学理科.files/image071.gif) 的等比数列 所以
的等比数列 所以 %20数学理科.files/image278.gif) …………8分
…………8分
(Ⅱ) 因为 %20数学理科.files/image280.gif) ,
…………10分
,
…………10分
所以 %20数学理科.files/image282.gif) ,
,%20数学理科.files/image284.gif) ,
,%20数学理科.files/image286.gif) ,……,
,……,%20数学理科.files/image288.gif)
叠加得 %20数学理科.files/image290.gif) 把
把%20数学理科.files/image140.gif) 代入得
代入得 %20数学理科.files/image144.gif) =
=%20数学理科.files/image294.gif) …………13分
…………13分
17. (本小题共14分)
%20数学理科.files/image296.gif) 如图,在正三棱柱
如图,在正三棱柱%20数学理科.files/image148.gif) 中,
中,%20数学理科.files/image150.gif) ,
,%20数学理科.files/image152.gif) 是
是%20数学理科.files/image154.gif) 的中点,点
的中点,点%20数学理科.files/image156.gif) 在
在%20数学理科.files/image158.gif) 上,
上,%20数学理科.files/image160.gif) 。
。
(Ⅰ)求%20数学理科.files/image162.gif) 所成角的正弦值;
所成角的正弦值;
(Ⅱ)证明%20数学理科.files/image164.gif) ;(Ⅲ) 求二面角
;(Ⅲ) 求二面角%20数学理科.files/image166.gif) 的大小.
的大小.
解:(Ⅰ)在正三棱柱%20数学理科.files/image148.gif) 中,
中, %20数学理科.files/image298.gif)
%20数学理科.files/image300.gif)
%20数学理科.files/image302.gif) ,又
,又%20数学理科.files/image152.gif) 是正△ABC边
是正△ABC边%20数学理科.files/image154.gif) 的中点,
的中点,%20数学理科.files/image300.gif)
%20数学理科.files/image305.gif)
,%20数学理科.files/image273.gif)
%20数学理科.files/image307.gif)
%20数学理科.files/image300.gif)
%20数学理科.files/image309.gif)
%20数学理科.files/image300.gif) ∠
∠%20数学理科.files/image311.gif) 为
为%20数学理科.files/image162.gif) 所成角
所成角
又 %20数学理科.files/image313.gif)
%20数学理科.files/image314.gif) sin∠
sin∠%20数学理科.files/image311.gif) =
=%20数学理科.files/image316.gif) …………5分
…………5分
(Ⅱ)证明: 依题意得 %20数学理科.files/image318.gif) ,
,%20数学理科.files/image320.gif) ,
,%20数学理科.files/image322.gif)
因为%20数学理科.files/image324.gif)
%20数学理科.files/image325.gif)
%20数学理科.files/image327.gif)
%20数学理科.files/image329.gif) 由(Ⅰ)知
由(Ⅰ)知%20数学理科.files/image331.gif) , 而
, 而%20数学理科.files/image329.gif)
%20数学理科.files/image333.gif) ,
,
所以 %20数学理科.files/image335.gif) 所以
所以%20数学理科.files/image164.gif) …………9分
…………9分
(Ⅲ) 过C作%20数学理科.files/image337.gif)
%20数学理科.files/image329.gif) 于
于%20数学理科.files/image091.gif) ,作
,作%20数学理科.files/image340.gif)
%20数学理科.files/image342.gif) 于
于%20数学理科.files/image344.gif) ,连接
,连接%20数学理科.files/image346.gif)
%20数学理科.files/image273.gif)
%20数学理科.files/image309.gif)
%20数学理科.files/image325.gif)
%20数学理科.files/image348.gif)
%20数学理科.files/image325.gif)
%20数学理科.files/image350.gif) , …………11分
, …………11分
又%20数学理科.files/image273.gif)
%20数学理科.files/image340.gif)
%20数学理科.files/image342.gif)
%20数学理科.files/image325.gif)
%20数学理科.files/image352.gif)
%20数学理科.files/image342.gif)
%20数学理科.files/image325.gif)
%20数学理科.files/image354.gif) 是所求二面角
是所求二面角%20数学理科.files/image166.gif) 的平面角
的平面角
%20数学理科.files/image273.gif)
%20数学理科.files/image356.gif) ,
,%20数学理科.files/image358.gif)
%20数学理科.files/image325.gif)
%20数学理科.files/image360.gif)
%20数学理科.files/image325.gif) 二面角
二面角%20数学理科.files/image166.gif) 的大小为
的大小为%20数学理科.files/image362.gif) …………14分
…………14分
18. (本小题共13分)
某校高二年级开设《几何证明选讲》及《坐标系与参数方程》两个模块的选修科目。每名学生可以选择参加一门选修,参加两门选修或不参加选修。已知有60%的学生参加过《几何证明选讲》的选修,有75%的学生参加过《坐标系与参数方程》的选修,假设每个人对选修科目的选择是相互独立的,且各人的选择相互之间没有影响。
(Ⅰ)任选一名学生,求该生参加过模块选修的概率;
(Ⅱ)任选3名学生,记%20数学理科.files/image168.gif) 为3人中参加过模块选修的人数,求
为3人中参加过模块选修的人数,求%20数学理科.files/image168.gif) 的分布列和期望。
的分布列和期望。
解:(Ⅰ)设该生参加过《几何证明选讲》的选修为事件A,
参加过《坐标系与参数方程》的选修为事件B, 该生参加过模块选修的概率为P,
则%20数学理科.files/image364.gif)
则 该生参加过模块选修的概率为0.9 …………6分
(另:%20数学理科.files/image366.gif) )
)
(Ⅱ) %20数学理科.files/image168.gif) 可能取值0,1,2,3
可能取值0,1,2,3
%20数学理科.files/image368.gif) =0.001,
=0.001,%20数学理科.files/image370.gif) =0.027
=0.027
%20数学理科.files/image372.gif) =0.243,
=0.243, %20数学理科.files/image374.gif) =0.729
…………10分
=0.729
…………10分
%20数学理科.files/image168.gif)
0
1
2
3
%20数学理科.files/image091.gif)
0.001
0.027
0.243
0.729
%20数学理科.files/image325.gif)
%20数学理科.files/image168.gif) 的分布列为
的分布列为
%20数学理科.files/image325.gif)
%20数学理科.files/image377.gif) …………13分
…………13分
19. (本小题共13分)
已知%20数学理科.files/image171.gif) 分别为椭圆
分别为椭圆%20数学理科.files/image173.gif) 的左、右焦点,直线
的左、右焦点,直线%20数学理科.files/image175.gif) 过点
过点%20数学理科.files/image177.gif) 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线%20数学理科.files/image179.gif) 垂直于直线
垂直于直线%20数学理科.files/image175.gif) ,垂足为
,垂足为%20数学理科.files/image181.gif) ,线段
,线段%20数学理科.files/image183.gif) 的垂直平分线交
的垂直平分线交%20数学理科.files/image185.gif) 于点M。(Ⅰ)求动点M的轨迹
于点M。(Ⅰ)求动点M的轨迹%20数学理科.files/image187.gif) 的方程;(Ⅱ)过点
的方程;(Ⅱ)过点%20数学理科.files/image177.gif) 作直线交曲线
作直线交曲线%20数学理科.files/image187.gif) 于两个不同的点P和Q,设=
于两个不同的点P和Q,设=%20数学理科.files/image189.gif) ,若
,若%20数学理科.files/image189.gif) ∈[2,3],求
∈[2,3],求%20数学理科.files/image192.gif) 的取值范围。
的取值范围。
解:(Ⅰ)设M%20数学理科.files/image379.gif) ,则
,则%20数学理科.files/image381.gif) ,由中垂线的性质知
,由中垂线的性质知%20数学理科.files/image383.gif)
%20数学理科.files/image325.gif) |
|%20数学理科.files/image385.gif) |=
|=%20数学理科.files/image387.gif) 化简得
化简得%20数学理科.files/image187.gif) 的方程为
的方程为%20数学理科.files/image389.gif) …………3分
…………3分
(另:由%20数学理科.files/image383.gif) 知曲线
知曲线%20数学理科.files/image187.gif) 是以x轴为对称轴,以
是以x轴为对称轴,以%20数学理科.files/image392.gif) 为焦点,以
为焦点,以%20数学理科.files/image175.gif) 为准线的抛物线
为准线的抛物线
所以 %20数学理科.files/image394.gif) ,
则动点M的轨迹
,
则动点M的轨迹%20数学理科.files/image187.gif) 的方程为
的方程为%20数学理科.files/image389.gif) )
)
(Ⅱ)设%20数学理科.files/image396.gif) ,由=
,由=%20数学理科.files/image189.gif) 知
知 %20数学理科.files/image398.gif) ①
①
又由%20数学理科.files/image396.gif) 在曲线
在曲线%20数学理科.files/image187.gif) 上知
上知 %20数学理科.files/image400.gif) ②
②
由 ① ② 解得%20数学理科.files/image402.gif) 所以
有
所以
有 %20数学理科.files/image404.gif) …………8分
…………8分
%20数学理科.files/image192.gif) =
=%20数学理科.files/image406.gif) =
=%20数学理科.files/image408.gif) =
=%20数学理科.files/image410.gif) …………10分
…………10分
设%20数学理科.files/image412.gif) 有
有%20数学理科.files/image414.gif) 在区间
在区间%20数学理科.files/image416.gif) 上是增函数,
上是增函数,
得%20数学理科.files/image418.gif) ,进而有
,进而有 %20数学理科.files/image420.gif) ,所以
,所以%20数学理科.files/image192.gif) 的取值范围是
的取值范围是%20数学理科.files/image422.gif) ……13分
……13分
20. (本小题共14分)
函 数 %20数学理科.files/image037.gif) 是 定 义 在R上 的 偶 函 数,且
是 定 义 在R上 的 偶 函 数,且%20数学理科.files/image195.gif) 时,
时,
%20数学理科.files/image424.jpg)
%20数学理科.files/image197.gif) ,记函数
,记函数%20数学理科.files/image037.gif) 的图像在
的图像在%20数学理科.files/image199.gif) 处的切线为
处的切线为%20数学理科.files/image425.gif) ,
,%20数学理科.files/image203.gif) 。
。
(Ⅰ) 求%20数学理科.files/image037.gif) 在
在%20数学理科.files/image205.gif) 上的解析式;
上的解析式;
(Ⅱ) 点列%20数学理科.files/image208.gif) 在
在%20数学理科.files/image201.gif) 上,
上,
%20数学理科.files/image210.gif) 依次为x轴上的点,
依次为x轴上的点,
如图,当%20数学理科.files/image212.gif) 时,点
时,点%20数学理科.files/image214.gif) 构成以
构成以%20数学理科.files/image216.gif) 为底边
为底边
的等腰三角形。若%20数学理科.files/image218.gif) ,求数列
,求数列%20数学理科.files/image220.gif) 的通项公式;
的通项公式;
(Ⅲ)在 (Ⅱ)的条件下,是否存在实数a使得数列%20数学理科.files/image220.gif) 是等差数列?如果存在,写出
是等差数列?如果存在,写出%20数学理科.files/image222.gif) 的一个值;如果不存在,请说明理由。
的一个值;如果不存在,请说明理由。
解:(Ⅰ) %20数学理科.files/image273.gif) 函数
函数%20数学理科.files/image037.gif) 是定义在R上的偶函数,且
是定义在R上的偶函数,且%20数学理科.files/image428.gif)
%20数学理科.files/image300.gif)
%20数学理科.files/image431.gif) ;
;%20数学理科.files/image300.gif)
%20数学理科.files/image037.gif) 是周期为2的函数
…………1分
是周期为2的函数
…………1分
%20数学理科.files/image273.gif)
%20数学理科.files/image433.gif)
%20数学理科.files/image300.gif)
%20数学理科.files/image435.gif)
由%20数学理科.files/image203.gif) 可知
可知%20数学理科.files/image437.gif) =-4
=-4 %20数学理科.files/image300.gif)
%20数学理科.files/image439.gif) ,
,%20数学理科.files/image441.gif) …………4分
…………4分
(Ⅱ) %20数学理科.files/image273.gif) 函数
函数%20数学理科.files/image037.gif) 的图像在
的图像在%20数学理科.files/image199.gif) 处的切线为
处的切线为%20数学理科.files/image201.gif) ,且
,且%20数学理科.files/image203.gif) ,
,
%20数学理科.files/image300.gif) 切线
切线%20数学理科.files/image201.gif) 过点
过点%20数学理科.files/image443.gif) 且斜率为1,
且斜率为1,%20数学理科.files/image300.gif) 切线
切线%20数学理科.files/image201.gif) 的方程为y=x+1
…………6分
的方程为y=x+1
…………6分
%20数学理科.files/image273.gif)
%20数学理科.files/image208.gif) 在
在%20数学理科.files/image201.gif) 上,有
上,有 %20数学理科.files/image446.gif) 即
即%20数学理科.files/image448.gif)
%20数学理科.files/image273.gif) 点
点%20数学理科.files/image214.gif) 构成以
构成以%20数学理科.files/image216.gif) 为底边的等腰三角形
为底边的等腰三角形%20数学理科.files/image300.gif)
%20数学理科.files/image450.gif) … ①
… ①
同理%20数学理科.files/image452.gif) … ② 两式相减 得
… ② 两式相减 得 %20数学理科.files/image454.gif)
%20数学理科.files/image273.gif)
%20数学理科.files/image456.gif)
%20数学理科.files/image458.gif)
%20数学理科.files/image300.gif)
%20数学理科.files/image460.gif) …………11分
…………11分
(Ⅲ) 假设%20数学理科.files/image220.gif) 是等差数列 ,则
是等差数列 ,则%20数学理科.files/image462.gif)
%20数学理科.files/image300.gif)
%20数学理科.files/image464.gif) …………14分
…………14分
故存在实数a使得数列%20数学理科.files/image220.gif) 是等差数列。
是等差数列。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com