题目列表(包括答案和解析)
（本题满分12分）
对甲、乙两种商品的重量的误差进行抽查，测得数据如下(单位：
)：
甲：13 15 14 14 9 14 21 9 10 11
乙：10 14 9 12 15 14 11 19 22 16
（1）画出样本数据的茎叶图，并指出甲，乙两种商品重量误差的中位数；
（2）计算甲种商品重量误差的样本方差；
（3）现从重量误差不低于15的乙种商品中随机抽取两件，求重量误差为19的商品被抽
中的概率。
（本题满分12分）
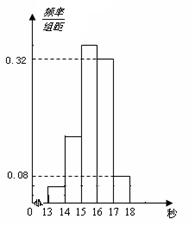
为了解某年段1000名学生的百米成绩情况，随机抽取了若干学生的百米成绩，成绩全部介于13秒与18秒之间，将成绩按如下方式分成五组：第一组[13，14）；第二组[14，15）;……;第五组[17，18].按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前3个组的频率之比为3∶8∶19，且第二组的频数为8.
（1）将频率当作概率，请估计该年段学生中百米成绩在[16，17）内的人数；
（2）求调查中随机抽取了多少个学生的百米成绩；
（3）若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1秒的概率.
（本题满分12分）为了了解某年段1000名学生的百米成绩情况，随机抽取了若
干学生的百米成绩，成绩全部介于13秒与18秒之间，将成绩按如下方式分成五组：第一组
[13，14）；第二组[14，15）;……;第五组[17，18].按上述分组方法得到的频率分布直方图如
图所示，已知图中从左到右的前3个组的频率之比为3∶8∶19，且第二组的频数为8.
（1）将频率当作概率，请估计该年段学生中百米成绩在[16，17）内的人数；
（2）求调查中随机抽取了多少个学生的百米成绩；
（3）若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1秒的概率.
（本题满分12分）某工厂有甲、乙两个生产小组，每个小组各有四名工人，某天该厂每位工人的生产情况如下表．
|
|
员工号 |
1 |
2 |
3 |
4 |
|
甲组
|
件数 |
9 |
11 |
1l
|
9
|
|
|
员工号 |
1 |
2 |
3 |
4 |
|
乙组
|
件数 |
b 9 |
8 |
10 |
9 |
(1)用茎叶图表示两组的生产情况；
(2)求乙组员工生产件数的平均数和方差；
(3)分别从甲、乙两组中随机选取一名员工的生产件数，求这两名员工的生产总件数为19的概率．
（注：方差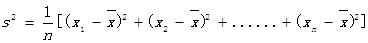
，其中
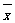为x1，x2，…，xn的平均数）
（本题满分12分）
对甲、乙两种商品的重量的误差进行抽查，测得数据如下(单位：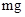
)：
甲：13 15 14 14 9 14 21 9 10 11
乙：10 14 9 12 15 14 11 19 22 16
（1）画出样本数据的茎叶图，并指出甲，乙两种商品重量误差的中位数；
（2）计算甲种商品重量误差的样本方差；
（3）现从重量误差不低于15的乙种商品中随机抽取两件，求重量误差为19的商品被抽
中的概率。
一、选择题：
题 号
1
2
3
4
5
6
7
8
9
10
11
12
答 案
B
A
D
B
D
B
C
C
A
B
D
A
二、填空题：
13．1 14．
15．5 16．
三、解答题:
17．解：（I）设“甲射击5次，有两次未击中目标”为事件A，则
答：甲射击5次，有两次未击中目标的概率为
…………5分
（Ⅱ）设“两人各射击4次，甲恰好击中目标2次，且乙恰好击中目标3次”为事件B，则
答：两人各射击4次，甲恰好击中目标2次，且乙恰好击中目标3次的概率为
………………10分
18．解：（I）
……2分
………………………………………4分
………………………………………6分
（II）由
得
的x的取值范围是
…………12分
19．解：（Ⅰ）因为四棱锥P―ABCD的底面是正方形，PA⊥底面ABCD，
则CD⊥侧面PAD
又
又
……………5分
（Ⅱ）建立如图所示的空间直角坐标系
又PA=AD=2，
|
则有
…………………………8分
…………12分
为奇函数，
………………………………………2分
的最小值为
的斜率为
，
，列表如下：
，
，
上的最大值是
、数列
的公差与公比.
分别加上1，1，3后得2，2+d,4+2d
……………4分
…………………………6分
①
，
，
②
………………9分
在N*是单调递增的，
恒成立的最小整数值为
……12分
，
，又曲线C过点Q（2，
），
………………5分
，∴M、B2、N三点共线
, ∴
垂直x轴时，不合题意
，①
的方程为 
②
代入双曲线方程得
，得
，
, ∴
，
………………12分