（09年临沂一模理）（12分）

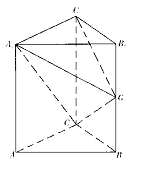
如图，在直棱柱ABC-A₁B₁C₁中，AC=BC=AA₁,∠ACB＝90º，G为BB₁的中点。

(1)求证：平面A₁CG⊥平面A₁GC₁;

(2)求平面ABC与平面A₁GC所成锐二面角的平面角的余弦值。

．（12分）

如图，△ABC内接于⊙O，过点A的直线交⊙O于点P，交BC的延长线于点D，

且AB2＝AP·AD

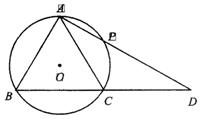
(1)求证：AB＝AC；

(2)如果∠ABC＝60°，⊙O的半径为1，且P为弧AC的中点，求AD的长．

在△ABC中，已知A(2, 0)，B(6, 0)，∠ACB＝90 º，那么顶点C的轨迹方程是            .

如图，在四棱椎P―ABCD中，底面ABCD是一直角梯形，∠BAD＝90º，

AD∥BC， AB＝BC＝AP=a，AD＝2a， PA⊥底面ABCD，

   （1）求异面直线BC与AP的距离；

   （2）求面PAB与面PDC所成二面角的余弦值。